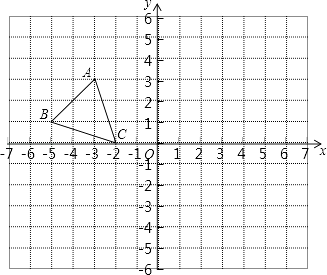题目内容
【题目】在△ABC中,∠ABC=2∠ACB,延长AB至点D,使BD=BC,点E是直线BC上一点,点F是直线AC上一点,连接DE.连接EF,且∠DEF=∠DBC.
(1)如图1,若∠D=∠EFC=15°,AB=![]() ,求AC的长.
,求AC的长.
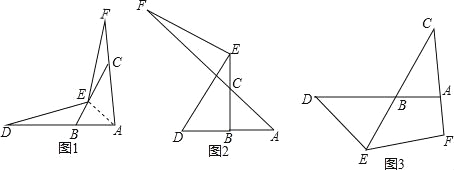
(2)如图2,当∠BAC=45°,点E为线段BC的延长线上,点F在线段AC的延长线上时,求证:CF=![]() BE.
BE.
(3)如图3,当∠BAC=90°,点E为线段CB的延长线上,点F在线段CA的延长线上时,猜想线段CF与线段BE的数量关系,并证明猜想的结论.
【答案】(1)3(2)证明见解析(3)CF=![]() BE
BE
【解析】
试题分析:(1)首先证明∠FEC=∠F=15°,推出∠ACB=30°,由此即可解决问题.
(2)如图2中,连接CD,作EM⊥EB交AF于M,作FN⊥BE于N,AF交DE于点O.∴由△EMC≌△ECD,推出EF=DE,再由△EFN≌△DEB,推出DB=EN=BC,推出BE=CN,推出△CFN是等腰直角三角形,由此即可解决问题.
(3)CF=![]() BE.如图3中,连接CD、DF、作NE⊥CE交AD的延长线于N,在线段CE上截取一点M,使得FM=FE.只要证明△EDN≌△CMF,推出NE=CF,即可解决问题.
BE.如图3中,连接CD、DF、作NE⊥CE交AD的延长线于N,在线段CE上截取一点M,使得FM=FE.只要证明△EDN≌△CMF,推出NE=CF,即可解决问题.
试题解析:(1)解:在△BDE中,∠D+∠DBE+∠BED=180°,
∵∠DEB+∠DEF+∠FEC=180°,∠DEF=∠DBC,
∴∠D=∠FEC=∠F=15°,
∴∠ACB=∠F+∠CEF=30°,
在Rt△ABC中,∵∠BAC=90°,AB=![]() ,∠ACB=30°,
,∠ACB=30°,
∴BC=2AB=2![]() ,
,
∴AC=![]() =3.
=3.
(2)证明:如图2中,连接CD,作EM⊥EB交AF于M,作FN⊥BE于N,AF交DE于点O.
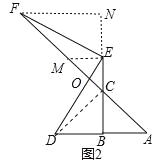
∵∠BAC=45°,∠ABC=2∠ACB,
∴∠ABC=90°,∠ACB=∠MCE=∠EMC=45°,
∴EM=EC,
∵BD=DC,
∴∠BDC=∠BCD=45°,
∴∠DCE=∠EMF=135°,
∵∠DEF=∠DBC=90°,∠FCD=∠DCA=90°,
∴∠OEF=∠OCD,∵∠EOF=∠COD,
∴∠OFE=∠ODC,
在△EMF和△ECD中,
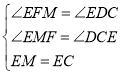 ,
,
∴△EMC≌△ECD,
∴EF=DE,
∵∠DEB+∠FEN=90°,∠EFN+∠FEN=90°,
∴∠EFN=∠DEB,
在△EFN和△DEB中,
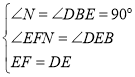 ,
,
∴△EFN≌△DEB,
∴DB=EN=BC,
∴BE=CN,
∵△CFN是等腰直角三角形,
∴CF=![]() CN=
CN=![]() BE.
BE.
(3)结论:CF=![]() BE.
BE.
理由:如图3中,连接CD、DF、作NE⊥CE交AD的延长线于N,在线段CE上截取一点M,使得FM=FE.
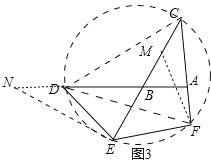
∵∠BAC=90°,∠ABC=2∠ACB,
∴∠ABC=60°,∠ACB=30°,
∵DB=BC,
∴∠DBC=120°,∠BDC=∠BCD=30°,
∴∠DBC=∠DEF=120°,∠DCA=∠DCB+∠ACB=60°,
∴∠DEF+∠DCF=180°,
∴E、F、C、D四点共圆,
∵∠DCE=∠ECF,
∴![]() ,
,
∴DE=EF=FM,
∵∠NEB=90°,∠NBE=∠ABC=60°,
∴∠N=∠ACM=30°,
∵∠DBC=∠BDE+∠DEB=∠DEB+∠FEM=∠DEB+∠FME,
∴∠BDE=∠FME,
∴∠NDE=∠FMC,
在△EDN和△FMC中,
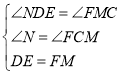 ,
,
∴△EDN≌△CMF,
∴NE=CF,
在Rt△NEB中,∵∠NEB=90°,∠N=30°,
∴NE=![]() BE,
BE,
∴CF=![]() BE.
BE.