题目内容
【题目】如图，已知正方形ABCD的对角线长为2
，将正方形ABCD沿直线EF折叠，则图中阴影部分的周长为（ ）
A. 8 B. 4 C. 8 D. 6
【答案】C
【解析】
首先由正方形ABCD的对角线长为2
，即可求得其边长为2，然后由折叠的性质，可得A′M=AM，D′N=DN，A′D′=AD，则可得图中阴影部分的周长为：A′M+BM+BC+CN+D′N+A′D′=AM+BM+BC+CN+DN+AD=AB+BC+CD+AD，继而求得答案．
解：∵正方形ABCD的对角线长为2，
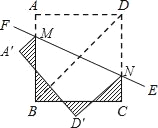
即BD=2，∠A=90°，AB=AD，∠ABD=45°，
∴AB=BDcos∠ABD=BDcos45°=2×
=2，
∴AB=BC=CD=AD=2，
由折叠的性质：A′M=AM，D′N=DN，A′D′=AD，
∴图中阴影部分的周长为：
A′M+BM+BC+CN+D′N+A′D′
=AM+BM+BC+CN+DN+AD
=AB+BC+CD+AD
=2+2+2+2
=8．
故选：C．
练习册系列答案
阅读快车系列答案
相关题目
