��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У�������y=��![]() x2+bx+c��x�ύ�ڵ�A��B����y�ύ�ڵ�C��ֱ��y=x+4����A��C���㣮
x2+bx+c��x�ύ�ڵ�A��B����y�ύ�ڵ�C��ֱ��y=x+4����A��C���㣮
��1���������ߵĽ���ʽ��
��2����AC�Ϸ�������������һ����P��
����ͼ1������P�˶���ijλ��ʱ����AP��AOΪ�ڱߵ�ƽ���ı��ε��ĸ�����ǡ��Ҳ���������ϣ������ʱ��P�����ꣻ
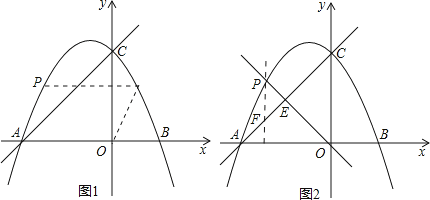
����ͼ2������O��P��ֱ��y=kx��AC�ڵ�E����PE��OE=3��8����k��ֵ��
���𰸡�
��1��
�⣺��ֱ��y=x+4����A��C���㣬
��A�������ǣ���4��0������C�����ǣ�0��4����
�֡������߹�A��C���㣬
��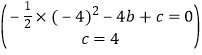 ����ã�
����ã�![]() ��
��
�������ߵĽ���ʽΪ![]() ��
��
��2��
�⣺����ͼ1
��![]() ��
��
�������ߵĶԳ�����ֱ��x=��1��
����AP��AOΪ�ڱߵ�ƽ���ı��εĵ��ĸ�����Qǡ��Ҳ���������ϣ�
��PQ��AO��PQ=AO=4��
��P��Q�����������ϣ�
��P��Q����ֱ��x=��1�Գƣ�
��P��ĺ������ǩ�3��
�൱x=��3ʱ��![]() ��
��
��P���������![]() ��
��
�ڹ�P����PF��OC��AC�ڵ�F����ͼ2
��PF��OC��
���PEF�ס�OEC��
��![]() ��
��
�֡�![]() ��
��
��![]() ��
��
���F��x��x+4����
��![]() ��
��
����ã�x2+4x+3=0����ã�x1=��1��x2=��3��
��x=��1ʱ��![]() ����x=��3ʱ��
����x=��3ʱ��![]() ��
��
��P��������![]() ��
��![]() ��
��
�֡ߵ�P��ֱ��y=kx�ϣ�
��![]() ��
��![]() ��
��
����������1����ֱ�ߵĽ���ʽy=x+4�����A�͵�C�����꣬��A��C������ֱ����y=��![]() x2+bx+c���b��c��ֵ���ɵõ������ߵĽ���ʽ��
x2+bx+c���b��c��ֵ���ɵõ������ߵĽ���ʽ��
��2��������AP��AOΪ�ڱߵ�ƽ���ı��εĵ��ĸ�����Qǡ��Ҳ���������ϣ���PQ��AO���ٸ��������ߵĶԳ���������P�ĺ����꣬�ɣ�1���е������߽���ʽ������������������꣬����ý⣻
�ڹ�P����PF��OC��AC�ڵ�F����ΪPF��OC�����ԡ�PEF�ס�OEC�������������ε����ʣ���Ӧ�ߵı�ֵ��ȿ����PF�ij�������������F��x��x+4��������![]() �������x��ֵ���ⷽ�����x��ֵ�ɵõ�P�����꣬����ֱ��y=kx�������k��ֵ��
�������x��ֵ���ⷽ�����x��ֵ�ɵõ�P�����꣬����ֱ��y=kx�������k��ֵ��
�����㾫�������ն��κ�����ͼ���ƽ���ı��ε��ж��������ǽ����ĸ�������Ҫ֪�����κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻��һֱ�߹�ƽ���ı������Խ��ߵĽ��㣬������ֱ�߱�һ��Ա߽��µ��߶��ԶԽ��ߵĽ���Ϊ�е㣬����������ֱ�߶��ȷִ�ƽ���ı��ε������

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�






