题目内容
(1998•安徽)已知数x1,x2,…xn的平均数是
,求(x1-
)+(x2-
)+…(xn-
)
. |
| x |
. |
| x |
. |
| x |
. |
| x |
分析:首先根据数x1,x2,…xn的平均数是
,得到x1+x2+…+xn=n
,最后代入(x1-
)+(x2-
)+…(xn-
)即可求解.
. |
| x |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
解答:解:∵数x1,x2,…xn的平均数是
,
∴x1+x2+…+xn=n
,
∴(x1-
)+(x2-
)+…(xn-
)
=x1+x2+…+xn-n
=n
-n
=0.
. |
| x |
∴x1+x2+…+xn=n
. |
| x |
∴(x1-
. |
| x |
. |
| x |
. |
| x |
=x1+x2+…+xn-n
. |
| x |
=n
. |
| x |
. |
| x |
=0.
点评:本题考查了算术平方根的求法,解题的关键是表示出所有数的和与平均数的关系.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
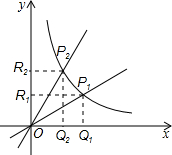 (1998•安徽)已知函数
(1998•安徽)已知函数