Question

（1998•安徽）已知函数y=

4

x

的图象和两条直线y=x，y=2x在第一象限内分别相交于P₁和P两点，过P₁分别作x轴、y轴的垂线P₁Q₁、P₂R₂，垂足分别为Q₁、R₁；过P₂分别作x轴、y轴的垂线P₂Q₂、P₂R₂，垂足分别为Q₂、R₂，求矩形OQ₁P₁R₁和OQ₂P₂R₂的周长比较它们的大小．

Answer 1

分析：分别解两个方程组程

y= 4 x y=x

和

y= 4 x y=2x

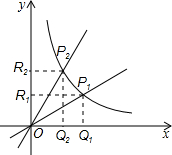
可确定点P₁的坐标为（2，2），点P₂的坐标为（

2

，2

2

）；再计算出矩形OQ₁P₁R₁的周长=2（2+2）=8，矩形OQ₂P₂R₂的周长=2（

2

+2

2

）=6

2

，然后利用平方法比较8与6

2

的大小即可．

解答：解：解方程组

y= 4 x y=x

得

x=2 y=2

或

x=-2 y=-2

，所以点P₁的坐标为（2，2）；
解方程组

y= 4 x y=2x

得

x= 2 y=2 2

或

x=- 2 y=-2 2

，所以点P₂的坐标为（

2

，2

2

）；
所以矩形OQ₁P₁R₁的周长=2（2+2）=8，矩形OQ₂P₂R₂的周长=2（

2

+2

2

）=6

2

，
因为8²=64，（6

2

）²=72，
所以矩形OQ₁P₁R₁的周长比矩形OQ₂P₂R₂的周长小．

点评：本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数的图象的交点坐标满足两个函数的解析式．也考查了矩形的周长．