题目内容
若△ABC和△A′B′C′的三边对应比值为1，则不正确的结论是
- A.△ABC≌△A′B′C′
- B.三边对应相等
- C.三对角对应相等
- D.△ABC与△A′B′C′不全等
D
分析：对应变的比值为1，即三边对应相等，所以两三角形全等，再根据全等三角形的对应边相等，全等三角形对应角相等即可对各选项作出正确判断．
解答：三边对应比值为1，即三边对应相等，故B正确；
所以△ABC≌△A′B′C′，故A选项正确；
全等三角形对应角相等，故C选项正确；
D、因为两三角形全等，所以本选项错误．
故选D．
点评：本题主要考查全等三角形的性质，根据三边对应比值为1判断出两三角形全等是解本题的关键．
分析：对应变的比值为1，即三边对应相等，所以两三角形全等，再根据全等三角形的对应边相等，全等三角形对应角相等即可对各选项作出正确判断．
解答：三边对应比值为1，即三边对应相等，故B正确；
所以△ABC≌△A′B′C′，故A选项正确；
全等三角形对应角相等，故C选项正确；
D、因为两三角形全等，所以本选项错误．
故选D．
点评：本题主要考查全等三角形的性质，根据三边对应比值为1判断出两三角形全等是解本题的关键．
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
利用三角形内角和，探究四边形内角和：
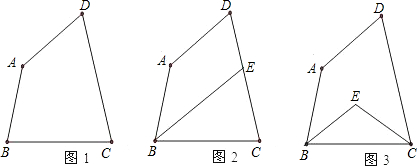
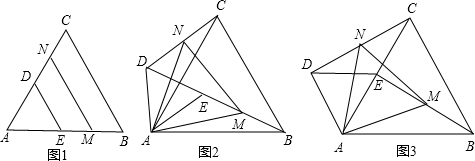
7、所示，若△ABC和△CDE是等边三角形，则△ACD和△BCE可以绕点