题目内容
7、所示，若△ABC和△CDE是等边三角形，则△ACD和△BCE可以绕点C
旋转60
度得到．分析：用全等三角形的判定，证明△ACD≌△BCE，观察两个三角形的旋转中心，旋转方向，旋转角，回答题目的问题．
解答：解：根据图形和旋转的性质可知，△ACD≌△BCE（SAS），
CE、CD之间的夹角是60度，即旋转角是60度，
点C是旋转中心．
所以△ACD和△BCE可以绕点C旋转60度得到．
填：C，60°．
CE、CD之间的夹角是60度，即旋转角是60度，
点C是旋转中心．
所以△ACD和△BCE可以绕点C旋转60度得到．
填：C，60°．
点评：本题考查旋转的性质．旋转变化前后，对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等．要注意旋转的三要素：①定点-旋转中心；②旋转方向；③旋转角度．
练习册系列答案
53随堂测系列答案
相关题目
4、如图所示，在△ABC和△DBC中，∠ACB=∠DBC=90°，点E是BC的中点，EF⊥AB，垂足为F，且AB=DE．
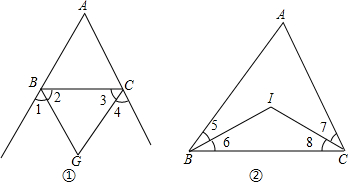
所示，若△ABC和△CDE是等边三角形，则△ACD和△BCE可以绕点________旋转________度得到．