题目内容
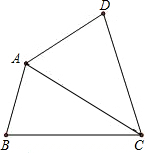 利用三角形内角和,探究四边形内角和:
利用三角形内角和,探究四边形内角和:如图,∠A、∠B、∠C、∠D是四边形的四个内角,连接AC,因为
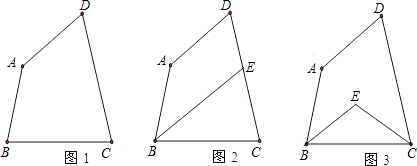
利用上述结论解题:四边形ABCD中,∠A=140°,∠D=80°.
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
分析:探究:从三角形的内角和考虑;
(1)根据四边形的内角和等于360°列式即可求解;
(2)先根据平行线的性质求出∠ABE与∠BED的度数,再根据角平分线的定义求出∠EBC的度数,然后根据三角形的一个外角等于与它不相邻的两个内角的和求解即可;
(3)先根据四边形的内角和等于360°求出∠ABC+∠BCD的度数,再根据角平分线的定义求出
(∠ABC+∠BCD)的度数,然后利用三角形的内角和定理列式即可求出∠BEC的度数.
(1)根据四边形的内角和等于360°列式即可求解;
(2)先根据平行线的性质求出∠ABE与∠BED的度数,再根据角平分线的定义求出∠EBC的度数,然后根据三角形的一个外角等于与它不相邻的两个内角的和求解即可;
(3)先根据四边形的内角和等于360°求出∠ABC+∠BCD的度数,再根据角平分线的定义求出
| 1 |
| 2 |
解答:解:探究:∵△ABC与△ACD的内角和都是180°,
∴∠A+∠B+∠C+∠D=360°,
即四边形内角和为360°;
(1)∵∠A=140°,∠D=80°,∠B=∠C,
∴140°+80°+2∠C=360°,
解得∠C=70°;
(2)∵∠A=140°,∠D=80°,BE∥AD,
∴∠ABE=180°-∠A=180°-140°=40°,
∠BED=180°-∠D=180°-80°=100°,
∵BE是∠ABC的角平分线,
∴∠EBC=∠ABE=40°,
在△BEC中,∠C=∠BED-∠EBC=100°-40°=60°;
(3)∵∠A=140°,∠D=80°,
∴∠ABC+∠BCD=360°-(∠A+∠D)=360°-(140°+80°)=140°,
∵BE、CE分别是∠ABC和∠BCD的角平分线,
∴∠EBC+∠ECB=
(∠ABC+∠BCD)=
×140°=70°,
在△BEC中,∠BEC=180°-(∠EBC+∠ECB)=180°-70°=110°.
∴∠A+∠B+∠C+∠D=360°,
即四边形内角和为360°;
(1)∵∠A=140°,∠D=80°,∠B=∠C,
∴140°+80°+2∠C=360°,
解得∠C=70°;
(2)∵∠A=140°,∠D=80°,BE∥AD,
∴∠ABE=180°-∠A=180°-140°=40°,
∠BED=180°-∠D=180°-80°=100°,
∵BE是∠ABC的角平分线,
∴∠EBC=∠ABE=40°,
在△BEC中,∠C=∠BED-∠EBC=100°-40°=60°;
(3)∵∠A=140°,∠D=80°,
∴∠ABC+∠BCD=360°-(∠A+∠D)=360°-(140°+80°)=140°,
∵BE、CE分别是∠ABC和∠BCD的角平分线,
∴∠EBC+∠ECB=
| 1 |
| 2 |
| 1 |
| 2 |
在△BEC中,∠BEC=180°-(∠EBC+∠ECB)=180°-70°=110°.
点评:本题考查了多边形的内角和公式的求解原理,平行线的性质以及三角形的内角和定理,角平分线的定义,仔细分析图形是解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
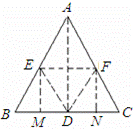
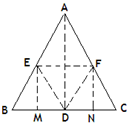 22、在“三角形内角和”的探究中课本中给我们了这样一种折叠方法,把三角形按如图的虚线折叠,可以得到了三角形的内角和等于180°,请你根据折叠过程证明这个结论.
22、在“三角形内角和”的探究中课本中给我们了这样一种折叠方法,把三角形按如图的虚线折叠,可以得到了三角形的内角和等于180°,请你根据折叠过程证明这个结论.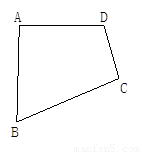
 利用三角形内角和,探究四边形内角和:
利用三角形内角和,探究四边形内角和: