��Ŀ����
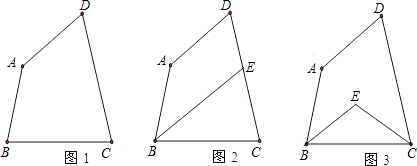
��ͼ1������ABC�͡�ADEΪ�ȱ������Σ�M��N�ֱ�EB��CD���е㣬��֤��CD=BE����AMN�ǵȱ������Σ�
��1�����ѡ�ADE��A����ת��ͼ2��λ��ʱ��CD=BE�Ƿ���Ȼ����������������֤����������������˵�����ɣ�
��2������ADE��A����ת��ͼ3��λ��ʱ����AMN�Ƿ��ǵȱ������Σ����ǣ������֤�����������AB=2ADʱ����ADE���ABC����AMN�����֮�ȣ������ǣ���˵�����ɣ�
��������1����������SAS�ж���ABE�ա�ACD��ȫ�������εĶ�Ӧ����ȣ�����CD=BE��
��2������֤����AMN�ǵȱ������Σ�AD=a����AB=2a��������֪�����ֱ���á�AMN�ı߳�����Ϊ��ADE����ABC����AMNΪ�ȱ������Σ���������ȵ��ڱ߳���ƽ���ıȣ�
��2������֤����AMN�ǵȱ������Σ�AD=a����AB=2a��������֪�����ֱ���á�AMN�ı߳�����Ϊ��ADE����ABC����AMNΪ�ȱ������Σ���������ȵ��ڱ߳���ƽ���ıȣ�
����⣺��1��CD=BE���������£���1�֣�
�ߡ�ABC�͡�ADEΪ�ȱ������Σ�
��AB=AC��AE=AD����BAC=��EAD=60�㣬
�ߡ�BAE=��BAC-��EAC=60��-��EAC��
��DAC=��DAE-��EAC=60��-��EAC��
���BAE=��DAC����3�֣�
���DAC�ա�EAB��SAS����
��CD=BE����4�֣�
��2����AMN�ǵȱ������Σ��������£���5�֣�
�ߡ�ABE�ա�ACD��
���ABE=��ACD
��M��N�ֱ���BE��CD���е㣬
��BM=
BE=
CD=CN��
��AB=AC����ABE=��ACD��
���ABM�ա�ACN��
��AM=AN����MAB=��NAC����6�֣�
���NAM=��NAC+��CAM=��MAB+��CAM=��BAC=60�㣬
���AMN�ǵȱ������Σ���7�֣�
��AD=a����AB=2a��
��AD=AE=DE��AB=AC��
��CE=DE��
�ߡ�ADEΪ�ȱ������Σ�
���DEC=120�㣬��ADE=60�㣬
���EDC=��ECD=30�㣬
���ADC=90�㣮��8�֣�
����Rt��ADC�У�AD=a����ACD=30�㣬
��CD=
a��
��NΪDC�е㣬
��DN=
a��
��AN=
=
=
a����9�֣�
�ߡ�ADE����ABC����AMNΪ�ȱ������Σ�
��S��ADE��S��ABC��S��AMN=a2����2a��2����
a��2=1��4��
=4��16��7��10�֣�
�ⷨ������AMN�ǵȱ������Σ��������£���5�֣�
�ߡ�ABE�ա�ACD��M��N�ֱ���BE��CD���е㣬
��AM=AN��NC=MB��
��AB=AC��
���ABM�ա�ACN��
���MAB=��NAC��
���NAM=��NAC+��CAM=��MAB+��CAM=��BAC=60�㣬
���AMN�ǵȱ������Σ���7�֣�
��AD=a����AD=AE=DE=a��AB=BC=AC=2a��
��֤BE��AC��
��BE=
=
=
a��
��EM=
a��
��AM=
=
=
a��
�ߡ�ADE����ABC����AMNΪ�ȱ������Σ�
��S��ADE��S��ABC��S��AMN=a2����2a��2����
a��2=1��4��
=4��16��7����10�֣�
�ߡ�ABC�͡�ADEΪ�ȱ������Σ�
��AB=AC��AE=AD����BAC=��EAD=60�㣬
�ߡ�BAE=��BAC-��EAC=60��-��EAC��
��DAC=��DAE-��EAC=60��-��EAC��
���BAE=��DAC����3�֣�
���DAC�ա�EAB��SAS����
��CD=BE����4�֣�
��2����AMN�ǵȱ������Σ��������£���5�֣�
�ߡ�ABE�ա�ACD��
���ABE=��ACD
��M��N�ֱ���BE��CD���е㣬
��BM=
| 1 |
| 2 |
| 1 |
| 2 |
��AB=AC����ABE=��ACD��
���ABM�ա�ACN��
��AM=AN����MAB=��NAC����6�֣�
���NAM=��NAC+��CAM=��MAB+��CAM=��BAC=60�㣬
���AMN�ǵȱ������Σ���7�֣�
��AD=a����AB=2a��
��AD=AE=DE��AB=AC��
��CE=DE��
�ߡ�ADEΪ�ȱ������Σ�
���DEC=120�㣬��ADE=60�㣬
���EDC=��ECD=30�㣬
���ADC=90�㣮��8�֣�
����Rt��ADC�У�AD=a����ACD=30�㣬
��CD=
| 3 |
��NΪDC�е㣬
��DN=
| ||
| 2 |
��AN=
| DN2+AD2 |
(
|
| ||
| 2 |
�ߡ�ADE����ABC����AMNΪ�ȱ������Σ�
��S��ADE��S��ABC��S��AMN=a2����2a��2����
| ||
| 2 |
| 7 |
| 4 |
�ⷨ������AMN�ǵȱ������Σ��������£���5�֣�
�ߡ�ABE�ա�ACD��M��N�ֱ���BE��CD���е㣬
��AM=AN��NC=MB��
��AB=AC��
���ABM�ա�ACN��
���MAB=��NAC��
���NAM=��NAC+��CAM=��MAB+��CAM=��BAC=60�㣬
���AMN�ǵȱ������Σ���7�֣�
��AD=a����AD=AE=DE=a��AB=BC=AC=2a��
��֤BE��AC��
��BE=
| AB2-AE2 |
| (2a)2-a2 |
| 3 |
��EM=
| ||
| 2 |
��AM=
| EM2+AE2 |
(
|
| ||
| 2 |
�ߡ�ADE����ABC����AMNΪ�ȱ������Σ�
��S��ADE��S��ABC��S��AMN=a2����2a��2����
| ||
| 2 |
| 7 |
| 4 |
���������⿼����ȫ�������ε��ж����ȱ������ε����ʣ����ɶ�������ת�����ʵ�֪ʶ���ۺ����ü�������֤������

��ϰ��ϵ�д�
�����Ŀ

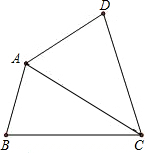 �����������ڽǺͣ�̽���ı����ڽǺͣ�
�����������ڽǺͣ�̽���ı����ڽǺͣ�