题目内容
如图,在平面直角坐标系中,有一直角△ABC,且A(0,5),B(-5,2),C(0,2),并已知△AA1C1是由△ABC经过旋转变换得到的.

(1)问由△ABC旋转得到的△AA1C1的旋转角的度数是多少?并写出旋转中心的坐标;
(2)请你画出仍以(1)中的旋转中心为旋转中心,将△AA1C1、△ABC分别按顺时针、逆时针各旋转90°的两个三角形,并写出变换后与A1相对应点A2的坐标;
(3)利用变换前后所形成图案证明勾股定理(设△ABC两直角边为 、
、 ,斜边为
,斜边为 ).
).

(1)问由△ABC旋转得到的△AA1C1的旋转角的度数是多少?并写出旋转中心的坐标;
(2)请你画出仍以(1)中的旋转中心为旋转中心,将△AA1C1、△ABC分别按顺时针、逆时针各旋转90°的两个三角形,并写出变换后与A1相对应点A2的坐标;
(3)利用变换前后所形成图案证明勾股定理(设△ABC两直角边为
 、
、 ,斜边为
,斜边为 ).
).解:(1)旋转角为90°,中心坐标为(-1,1) ……… 3分
(2)如图,点 对应点
对应点 的坐标为(-2,-3) ……… 5分
的坐标为(-2,-3) ……… 5分

(3)正方形 面积:
面积: ,
,
正方形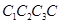 的面积:
的面积: ,
,
设,AC= ,BC=
,BC= ,AB=c
,AB=c
则,

∴ …………… 9分
…………… 9分
(2)如图,点
 对应点
对应点 的坐标为(-2,-3) ……… 5分
的坐标为(-2,-3) ……… 5分
(3)正方形
 面积:
面积: ,
,正方形
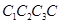 的面积:
的面积: ,
,设,AC=
 ,BC=
,BC= ,AB=c
,AB=c则,


∴
 …………… 9分
…………… 9分(1)图象的旋转可以利用某点的旋转来找到旋转的角度和旋转中心;
(2)在解决题中第2问时,还需认真分析、观察旋转前后图案的特征,并利用其面积关系来验证勾股定理.
(3)利用正方形的面积的不同计算方法进行验证勾股定理
(2)在解决题中第2问时,还需认真分析、观察旋转前后图案的特征,并利用其面积关系来验证勾股定理.
(3)利用正方形的面积的不同计算方法进行验证勾股定理

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 ,四边形
,四边形 的四个顶点都在格点上,
的四个顶点都在格点上, 为
为 边的中点,若把四边形
边的中点,若把四边形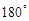 .
. 旋转后的对应点为
旋转后的对应点为 ,则
,则 ;
;


