Question

【题目】如图，在和中，，，，，连接，交于点，连接，下列结论：①；②；③平分；④平分，其中正确的序号是__________．

Answer 1

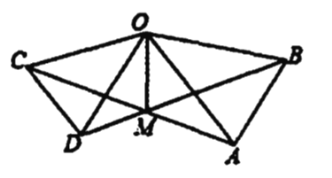
【答案】①②④

【解析】

由SAS证明△AOC≌△BOD得出∠OCA=∠ODB，AC=BD，①正确；

由全等三角形的性质得出∠OAC=∠OBD，由三角形的外角性质得：∠AMB+∠OAC=∠AOB+∠OBD，得出∠AMB=∠AOB=40°，②正确；

作OG⊥MC于G，OH⊥MB于H，如图所示：则∠OGC=∠OHD=90°，由AAS证明△OCG≌△ODH（AAS），得出OG=OH，由角平分线的判定方法得出MO平分∠BMC，④正确；

先假设OM平分∠AOD，推出OA=OC与条件中相矛盾，推出③错误．

解：∵∠AOB=∠COD=40，

∴∠AOB+∠AOD=∠COD+∠AOD，

即∠AOC=∠BOD，

在△AOC和△BOD中，

，

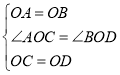∴△AOC△BOD，

∴∠OCA=∠ODB，AC=BD，①正确；

∵△AOC△BOD

∴∠OAC=∠OBD，

由三角形的外角性质得：∠AMB+∠OAC=∠AOB+∠OBD，

∴∠AMB=∠AOB=40，

∴∠CMD=∠AMB=40，②正确；

作OG⊥MC于G，OH⊥MB于H，如图2所示：

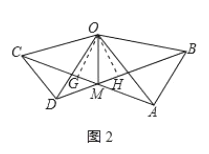
则∠OGC=∠OHD=90，

在△OCG和△ODH中，

，

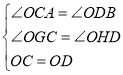∴△OCG△ODH，

∴OG=OH，

∵OG⊥MC，OH⊥MB

∴MO平分∠BMC，④正确；

∵∠AOB=∠COD，

假设OM平分∠AOD，

∵OM平分∠AOD，

∴∠AOM=∠DOM，

∵△AOC≌△BOD，

∴∠COM=∠BOM，

∵MO平分∠BMC，

∴∠CMO=∠BMO，

在△COM和△BOM中，

∴△COM≌△BOM(ASA)，

∴OB=OC，

∵OA=OB，

∴OA=OC，

与OA>OC矛盾，

故假设不成立，OM不平分∠AOD

∴③错误；

故答案为：①②④