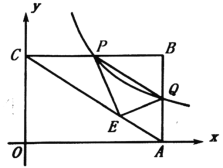
题目内容
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的边
的边![]() 、
、![]() 分别在轴和y轴上,
分别在轴和y轴上,![]() ,
,![]() ,点Q是
,点Q是![]() 边上一个动点,过点Q的反比例函数
边上一个动点,过点Q的反比例函数![]() 与
与![]() 边交于点P.若将
边交于点P.若将![]() 沿
沿![]() 折叠,点B的对应点E恰好落在对角线
折叠,点B的对应点E恰好落在对角线![]() 上,则此时反比例函数的解析式是_______.
上,则此时反比例函数的解析式是_______.
【答案】![]()
【解析】
由题意得:直线AC的函数解析式为:y=![]() x+4,设点E坐标是:(x,
x+4,设点E坐标是:(x,![]() x+4),作EM⊥BC,EN⊥AB,则ME=4-(
x+4),作EM⊥BC,EN⊥AB,则ME=4-(![]() x+4)=
x+4)= ![]() x,NE=6-x,易证:PME~QNE,进而得到:
x,NE=6-x,易证:PME~QNE,进而得到: ,求出点E坐标是:(
,求出点E坐标是:(![]() ,
,![]() ),在RtPME中,PM2+ME2=PE2,列出方程,即可求出k得值,进而得到答案.
),在RtPME中,PM2+ME2=PE2,列出方程,即可求出k得值,进而得到答案.
∵在平面直角坐标系![]() 中,矩形
中,矩形![]() 的边
的边![]() 、
、![]() 分别在x轴和y轴上,
分别在x轴和y轴上,![]() ,
,![]() ,
,
∴点A坐标是:(6,0),点C坐标是:(0,4),
设直线AC的函数解析式为:y=kx+b,把(6,0),(0,4),代入得:![]()
解得: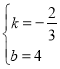 ,
,
∴直线AC的函数解析式为:y=![]() x+4,
x+4,
∵点E恰好落在对角线![]() 上,
上,
设点E坐标是:(x,![]() x+4),作EM⊥BC,EN⊥AB,则ME=4-(
x+4),作EM⊥BC,EN⊥AB,则ME=4-(![]() x+4)=
x+4)= ![]() x,NE=6-x,∠PEM=∠QEN,∠PME=∠QNE=90°,
x,NE=6-x,∠PEM=∠QEN,∠PME=∠QNE=90°,
∴PME~
∴![]() ,
,
∵点Q是![]() 边上一个动点,过点Q的反比例函数
边上一个动点,过点Q的反比例函数![]() 与
与![]() 边交于点P,
边交于点P,
∴Q(6,![]() ),P(
),P(![]() ,4),
,4),
∵![]() 沿
沿![]() 折叠得到
折叠得到![]()
∴PB=PE=6-![]() ,BQ=EQ=4-
,BQ=EQ=4-![]() ,
,
∴ ,即:
,即: ,解得:x=
,解得:x=![]() ,
,
∴点E坐标是:(![]() ,
,![]() )
)
∵在RtPME中,PM2+ME2=PE2,
∴![]() ,解得:k=
,解得:k=![]() ,
,
∴反比例函数的解析式为:![]() ,
,
故答案是:![]() .
.


【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |

(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?
【题目】某商店购进一批单价为8元的商品,经调研发现,这种商品每天的销售量y(件)是关于销售单价x(元)的一次函数,其关系如下表:
x(元) | 10 | 11 | 12 | 13 | 14 |
y(件) | 100 | 90 | 80 | 70 | 60 |
(1)求y与x之间的关系式;
(2)设商店每天销售利润为w(元),求出w与x之间的关系式,并求出每天销售单价定为多少时利润最大?