题目内容
【题目】如图，已知某学校A与直线公路BD相距3000米，且与该公路上一个车站D相距5000米，现要在公路边建一个超市C，使之与学校A及车站D的距离相等，那么该超市与车站D的距离是多少米？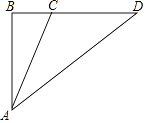 
【答案】解：根据题意得：AC=CD，∠ABD=90°．
在直角三角形ABD中，
∵AB=3000，AD=5000，
∴BD= 
=4000（m），
设CD=AC=x米，BC=4000﹣x（米），
在Rt△ABC中，AC2=AB2+BC2，
即x2=30002+（4000﹣x）2
解得：x=3125，
答：该超市与车站D的距离是3125米．
【解析】根据题意，AC=CD，∠ABD=90°，由AB、AD的长易求BD，设CD=x米，则AC=x，BC=BD﹣x．在直角三角形ABC中运用勾股定理得关系式求解．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
