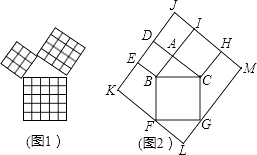
��Ŀ����
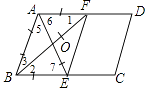
����Ŀ����ͼ���ڸ�����һ��ƽ���ı���ֽƬ����һ�����Σ��ס������˵��������£� �ף�����AC����AC�Ĵ�ֱƽ����MN�ֱ�AD��AC��BC��M��O��N������AN��CM�����ı���ANCM�����Σ�
�ң��ֱ�����A����B��ƽ����AE��BF���ֱ�BC��AD��E��F������EF�����ı���ABEF�����Σ�
�������˵��������жϣ� ��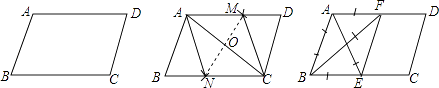
A.����ȷ���Ҵ���
B.����ȷ���״���
C.�ס��Ҿ���ȷ
D.�ס��Ҿ�����
���𰸡�C
���������⣺��������ȷ��
���ı���ABCD��ƽ���ı��Σ�
��AD��BC��
���DAC=��ACN��
��MN��AC�Ĵ�ֱƽ���ߣ�
��AO=CO��
�ڡ�AOM�͡�CON�� 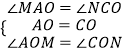 ��
��
���AOM�ա�CON��ASA����
��MO=NO��
���ı���ANCM��ƽ���ı��Σ�
��AC��MN��
���ı���ANCM�����Σ�
�ҵ�������ȷ��
��AD��BC��
���1=��2����6=��7��
��BFƽ�֡�ABC��AEƽ�֡�BAD��
���2=��3����5=��6��
���1=��3����5=��7��
��AB=AF��AB=BE��
��AF=BE
��AF��BE����AF=BE��
���ı���ABEF��ƽ���ı��Σ�
��AB=AF��
��ƽ���ı���ABEF�����Σ�
��ѡ��C��
����֤����AOM�ա�CON��ASA�����ɵ�MO=NO���ٸ��ݶԽ�����ƽ�ֵ��ı�����ƽ���ı��ο��ж��ж��ı���ANCM��ƽ���ı��Σ�����AC��MN���ɸ��ݶԽ����ഹֱ���ı����������ж���ANCM�����Σ��ı���ABCD��ƽ���ı��Σ��ɸ��ݽ�ƽ���ߵĶ����ƽ���ߵĶ��壬���AB=AF�������ı���ABEF�����Σ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��Ϊ�˷���ũ��չũҵ���������ҶԹ���ũ����ũ������ũ���ۼ�13%������������ij��ũ����˾�O���ʽ�130��Ԫ������һ���Թ���A��B�����ͺŵ��ո��30̨�������г�������Щ�ո������ȫ�����ۣ�ȫ�����ۺ���������15��Ԫ�����У��ո���Ľ��ۺ��ۼۼ��±���
A���ո�� | B���ո�� | |
���ۣ���Ԫ/̨�� | 5.3 | 3.6 |
�ۼۣ���Ԫ/̨�� | 6 | 4 |
�蹫˾�ƻ�����A���ո��x̨���ո��ȫ�����ۺ�˾��õ�����Ϊy��Ԫ��
��1����д��y��x�ĺ�����ϵʽ��
��2����ũ����˾���ļ��ֹ����ո���ķ����ɹ�ѡ��
��3��ѡ�����ֹ����ո���ķ�����ũ����˾���������������Ƕ��٣���������£�������30̨�ո��������ũ����õ����������ܶ�WΪ������Ԫ��