题目内容
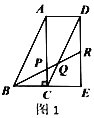
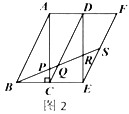
【题目】如图,点D是等边△ABC内一点,将线段AD绕着点A逆时针旋转60°得到线段AE,连结CD并延长交AB于点F,连结BD,CE.
(1)求证:△ACE≌△ABD;
(2)当CF⊥AB时,∠ADB=140°,求∠ECD的度数.
【答案】(1)详见解析;(2)50°
【解析】
(1)由“SAS”可证△ACE≌△ABD;
(2)由等边三角形的性质和等腰三角形的性质可求∠BDF=70°,即可得∠ABD=20°,由全等三角形的性质可得∠ACE=20°,即可求解.
解:(1)∵△ABC是等边三角形
∴AC=AB,∠CAB=60°
∵将线段AD绕着点A逆时针旋转60°得到线段AE
∴AE=AD,∠EAD=∠CAB=60°
∴∠EAC=∠DAB,且AC=AB,AE=AD
∴△ACE≌△ABD(SAS)
(2)∵CF⊥AB,AC=BC
∴DF垂直平分AB,∠ACF=![]() ∠ACB=30°
∠ACB=30°
∴AD=DB,且DF⊥AB
∴∠ADF=∠BDF=![]() ∠ADB=70°
∠ADB=70°
∴∠ABD=20°
∵△ACE≌△ABD
∴∠ABD=∠ACE=20°
∴∠ECD=∠ACE+∠ACF=50°

 计算高手系列答案
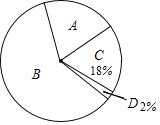
计算高手系列答案【题目】某中学的一个数学兴趣小组在本校学生中开展了主题为“雾霾知多少”的专题调查括动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“A.非常了解”、“B.比较了解”、“C.基本了解”、“D.不太了解”四个等级,将所得数据进行整理后,绘制成如下两幅不完整的统计图表,请你结合图表中的信息解答下列问题
等级 | A | B | C | D |
频数 | 40 | 120 | 36 | n |
频率 | 0.2 | m | 0.18 | 0.02 |
(1)表中m= ,n= ;
(2)扇形统计图中,A部分所对应的扇形的圆心角是 °,所抽取学生对丁雾霾了解程度的众数是 ;
(3)若该校共有学生1500人,请根据调查结果估计这些学生中“比较了解”人数约为多少?
【题目】某校为了解八年级学生课外阅读情况,随机抽取20名学生平均每周用于课外阅读读的时间(单位:![]() ),过程如下:
),过程如下:
(收集数据)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
(整理数据)
课外阅读时间 |
|
|
|
|
等级 |
|
|
|
|
人数 | 3 |
| 8 |
|
(分析数据)
平均数 | 中位数 | 众数 |
80 |
|
|
请根据以上提供的信息,解答下列问题:
(1)填空:![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)如果每周用于课外读的时间不少于![]() 为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?
为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?