题目内容
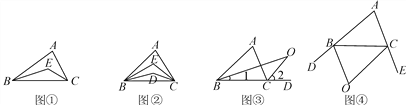
【题目】【问题】如图①,在△ABC中,BE平分∠ABC,CE平分∠ACB,若∠A=80°,则∠BEC=__ __;若∠A=n°,则∠BEC=__ _.
【探究】
(1)如图②,在△ABC中,BD,BE三等分∠ABC,CD,CE三等分∠ACB.若∠A=n°,则∠BEC=____;
(2)如图③,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC和∠A有怎样的关系?请说明理由;
(3)如图④,O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
【答案】问题:130°,90°+![]() n°探究:(1)60°+
n°探究:(1)60°+![]() n°(2)∠BOC=
n°(2)∠BOC=![]() ∠A. (3)∠BOC=90°-
∠A. (3)∠BOC=90°-![]() ∠A
∠A
【解析】试题分析:问题:利用三角形的内角和等于180°求出∠ABC+∠ACB,再利用角平分线的定义求出∠EBC+∠ECB,然后根据三角形的内角和等于180°列式计算即可得解;将∠A的度数换成n°,然后求解即可;
探究:(1)利用三角形的内角和等于180°求出∠ABC+∠ACB,再利用三等分角求出∠EBC+∠ECB,然后根据三角形的内角和等于180°列式计算即可得解;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠ACD和∠OCD,再根据角平分线的定义可得∠ABC=2∠OBC,∠ACD=2∠OCD,然后整理即可得解;
(3)根据平角的定义以及角平分线的定义表示出∠OBC和∠OCB,然后根据三角形的内角和定理列式表示出∠BOC,然后整理即可得解.
试题解析:【问题】解:∵∠A=80°,
∴∠ABC+∠ACB=180°-∠A=180°-80°=100°,
∵BE平分∠ABC,CE平分∠ACB,
∴∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,
∠ACB,
∴∠EBC+∠ECB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×100°=50°,
×100°=50°,
∴∠BEC=180°-(∠EBC+∠ECB)=180°-50°=130°;
由三角形的内角和定理得,∠ABC+∠ACB=180°-∠A=180°-n°,
∵BE平分∠ABC,CE平分∠ACB,
∴∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,
∠ACB,
∴∠EBC+∠ECB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×(180°-n°)=90°-
×(180°-n°)=90°-![]() n°,
n°,
∴∠BEC=180°-(∠EBC+∠ECB)=180°-(90°-![]() n°)=90°+
n°)=90°+![]() n°;
n°;
探究:解:(1)由三角形的内角和定理得,∠ABC+∠ACB=180°-∠A=180°-n°,
∵BD,BE三等分∠ABC,CD,CE三等分∠ACB,
∴∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,
∠ACB,
∴∠EBC+∠ECB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×(180°-n°)=120°-
×(180°-n°)=120°-![]() n°,
n°,
∴∠BEC=180°-(∠EBC+∠ECB)=180°-(120°-![]() n°)=60°+
n°)=60°+![]() n°;
n°;
(2)∠BOC=![]() ∠A.
∠A.
理由如下:由三角形的外角性质得,∠ACD=∠A+∠ABC,
∠OCD=∠BOC+∠OBC,
∵O是∠ABC与外角∠ACD的平分线BO和CO的交点,
∴∠ABC=2∠OBC,∠ACD=2∠OCD,
∴∠A+∠ABC=2(∠BOC+∠OBC),
∴∠A=2∠BOC,
∴∠BOC=![]() ∠A;
∠A;
(3)∵O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,
∴∠OBC=![]() (180°-∠ABC)=90°-
(180°-∠ABC)=90°-![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() (180°-∠ACB)=90°-
(180°-∠ACB)=90°-![]() ∠ACB,
∠ACB,
在△OBC中,∠BOC=180°-∠OBC-∠OCB=180°-(90°-![]() ∠ABC)-(90°-
∠ABC)-(90°-![]() ∠ACB)=
∠ACB)=![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
由三角形的内角和定理得,∠ABC+∠ACB=180°-∠A,
∴∠BOC=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A.
∠A.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案