题目内容
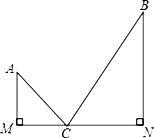
【题目】如图:知:AM⊥MN,BN⊥MN,垂足分别为M,N,点C是MN上使AC+BC的值最小的点.若AM=3,BN=5,MN=15,则AC+BC=______.
【答案】17
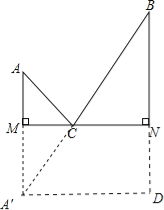
【解析】试题分析:以MN为轴作A点对称点A′,连接A′B交MN于C,则A′B就是AC+BC最小值;根据勾股定理求得A′B的长,即可求得AC+BC的最小值.
解:作A点关于直线MN的对称点A′,连接A′B交MN于C,则AC+BC=A′C+BC=A′B,A′B就是AC+BC的最小值;
延长BN使ND=A′M,连接A′D,
∵AM⊥MN,BN⊥MN,
∴AA′∥BD,
∴四边形A′DNM是矩形,
∴ND=AM=3,A′D=MN=15,
∴BD=BN+ND=5+3=8,
∴A′B=![]() =17,
=17,
∴AC+BC=17,
故答案为17.

练习册系列答案
相关题目