Question

【题目】在一个三角形中，如果一个角是另一个角的3倍，这样的三角形我们称之为“灵动三角形”．如，三个内角分别为120°，40°，20°的三角形是“灵动三角形”．

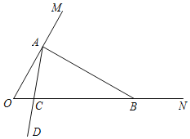
如图，∠MON＝60°，在射线OM上找一点A，过点A作AB⊥OM交ON于点B，以A为端点作射线AD，交线段OB于点C（规定0°< ∠OAC < 90°）．

（1）∠ABO的度数为　 　°，△AOB　 　（填“是”或“不是”灵动三角形）；

（2）若∠BAC＝60°，求证：△AOC为“灵动三角形”；

（3）当△ABC为“灵动三角形”时，求∠OAC的度数．

Answer 1

【答案】（1）30°；（2）详见解析；（3）∠OAC=80°或52.5°或30°.

【解析】

（1）根据垂直的定义、三角形内角和定理求出∠ABO的度数，根据“智慧三角形”的概念判断；
（2）根据“智慧三角形”的概念证明即可；
（3）分点C在线段OB和线段OB的延长线上两种情况，根据“智慧三角形”的定义计算．

（1）答案为：30°；是；

（2）∵AB⊥OM

∴∠BAO＝90°

∵∠BAC＝60°

∴∠OAC＝∠BAO-∠BAC=30°

∵∠MON＝60°

∴∠ACO＝180°-∠OAC-∠MON＝90°

∴∠ACO＝3∠OAC，

∴△AOC为“灵动三角形”；

（3）设∠OAC= x°则∠BAC=90-x, ∠ACB=60+x , ∠ABC＝30°

∵△ABC为“智慧三角形”，

Ⅰ、当∠ABC＝3∠BAC时，°，

∴30＝3（90-x）， ∴x=80

Ⅱ、当∠ABC＝3∠ACB时，

∴30=3（60+x） ∴x= -50 （舍去）

∴此种情况不存在，

Ⅲ、当∠BCA＝3∠BAC时，

∴60+x＝3（90-x），

∴x＝52.5°，

Ⅳ、当∠BCA＝3∠ABC时，

∴60+x＝90°，

∴x＝30°，

Ⅴ、当∠BAC＝3∠ABC时，

∴90-x＝90°，

∴x＝0°（舍去）

Ⅵ、当∠BAC＝3∠ACB时，

∴90-x＝3（60+x），

∴x= -22.5（舍去），

∴此种情况不存在，

∴综上所述：∠OAC=80°或52.5°或30°。