题目内容
【题目】如图，P为反比例函数y= 
（k＞0）在第一象限内图象上的一点，过点P分别作x轴，y轴的垂线交一次函数y=﹣x﹣4的图象于点A，B．若∠AOB=135°，则k的值是（ ）
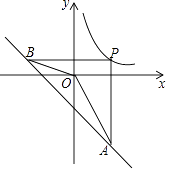
A.2
B.4
C.6
D.8
【答案】D
【解析】解：方法1、作BF⊥x轴，OE⊥AB，CQ⊥AP；设P点坐标（n， 
），
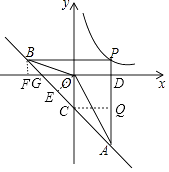
∵直线AB函数式为y=﹣x﹣4，PB⊥y轴，PA⊥x轴，
∴C（0，﹣4），G（﹣4，0），
∴OC=OG，
∴∠OGC=∠OCG=45°
∵PB∥OG，PA∥OC，
∴∠PBA=∠OGC=45°，∠PAB=∠OCG=45°，
∴PA=PB，
∵P点坐标（n， ），
∴OD=CQ=n，
∴AD=AQ+DQ=n+4；
∵当x=0时，y=﹣x﹣4=﹣4，
∴OC=DQ=4，GE=OE= 
OC= 
；
同理可证：BG= 
BF= PD= 
，
∴BE=BG+EG= + ；
∵∠AOB=135°，
∴∠OBE+∠OAE=45°，
∵∠DAO+∠OAE=45°，
∴∠DAO=∠OBE，
∵在△BOE和△AOD中， 
，
∴△BOE∽△AOD；
∴ 
= 
，即 
= 
；
整理得：nk+2n2=8n+2n2，化简得：k=8；
所以答案是：D．
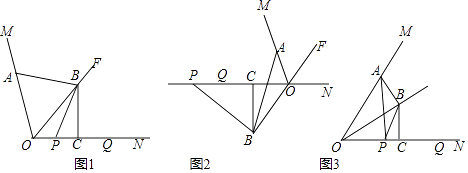
方法2、如图1，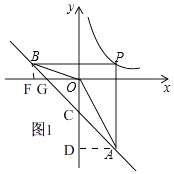 
过B作BF⊥x轴于F，过点A作AD⊥y轴于D，
∵直线AB函数式为y=﹣x﹣4，PB⊥y轴，PA⊥x轴，
∴C（0，﹣4），G（﹣4，0），
∴OC=OG，
∴∠OGC=∠OCG=45°
∵PB∥OG，PA∥OC，
∴∠PBA=∠OGC=45°，∠PAB=∠OCG=45°，
∴PA=PB，
∵P点坐标（n， ），
∴A（n，﹣n﹣4），B（﹣4﹣ ， ）
∴AD=AQ+DQ=n+4；
∵当x=0时，y=﹣x﹣4=﹣4，
∴OC=4，
当y=0时，x=﹣4．
∴OG=4，
∵∠AOB=135°，
∴∠BOG+∠AOC=45°，
∵直线AB的解析式为y=﹣x﹣4，
∴∠AGO=∠OCG=45°，
∴∠BGO=∠OCA，∠BOG+∠OBG=45°，
∴∠OBG=∠AOC，
∴△BOG∽△OAC，
∴ 
= 
，
∴ 
= 
，
在等腰Rt△BFG中，BG= BF= ，
在等腰Rt△ACD中，AC= AD= n，
∴ 
，
∴k=8，
所以答案是：D．
【考点精析】通过灵活运用反比例函数的图象和相似三角形的判定，掌握反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点；相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）即可以解答此题．
