题目内容
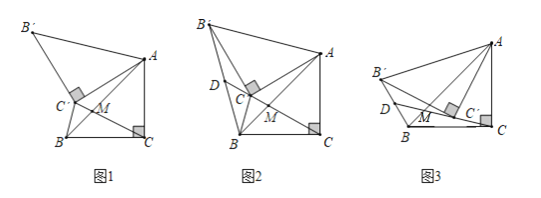
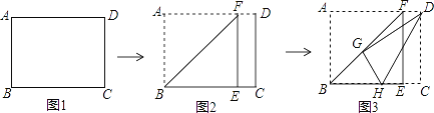
【题目】如图1,有一张矩形纸片ABCD,已知AB=10,AD=12,现将纸片进行如下操作:现将纸片沿折痕BF进行折叠,使点A落在BC边上的点E处,点F在AD上(如图2);然后将纸片沿折痕DH进行第二次折叠,使点C落在第一次的折痕BF上的点G处,点H在BC上(如图3),给出四个结论:
①AF的长为10;②△BGH的周长为18;③![]() =
=![]() ;④GH的长为5,
;④GH的长为5,
其中正确的结论有________.(写出所有正确结论的番号)
【答案】①③④
【解析】
过G点作MN∥AB,交AD、BC于点M、N,可知四边形ABEF为正方形,可求得AF的长,可判断①,且△BNG和△FMG为等腰三角形,设BN=x,则可表示出GN、MG、MD,利用折叠的性质可得到CD=DG.在Rt△MDG中,利用勾股定理可求得x,再利用△MGD∽△NHG,可求得NH、GH和HC,则可求得BH,容易判断②③④,可得出答案.
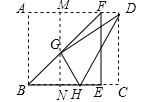
如图,过点G作MN∥AB,分别交AD、BC于点M、N.
∵四边形ABCD为矩形,∴AB=CD=10,BC=AD=12,由折叠可得:AB=BE,且∠A=∠ABE=∠BEF=90°,∴四边形ABEF为正方形,∴AF=AB=10,故①正确;
∵MN∥AB,∴△BNG和△FMG为等腰直角三角形,且MN=AB=10,设BN=x,则GN=AM=x,MG=MN﹣GN=10﹣x,MD=AD﹣AM=12﹣x,又由折叠的可知DG=DC=10.在Rt△MDG中,由勾股定理可得:MD2+MG2=GD2,即(12﹣x)2+(10﹣x)2=102,解得:x=18(舍去),x=4,∴GN=BN=4,MG=6,MD=8,又∠DGH=∠C=∠GMD=90°,∴∠NGH+∠MGD=∠MGD+∠MDG=90°,∴∠NGH=∠MDG,且∠DMG=∠GNH,∴△MGD∽△NHG,∴![]() ,即
,即![]() ,∴NH=3,GH=CH=5,∴BH=BC﹣HC=12﹣5=7,故④正确;
,∴NH=3,GH=CH=5,∴BH=BC﹣HC=12﹣5=7,故④正确;
又∵△BNG和△FMG为等腰直角三角形,且BN=4,MG=6,∴BG=4![]() ,GF=6
,GF=6![]() ,∴△BGH的周长=BG+GH+BH=4
,∴△BGH的周长=BG+GH+BH=4![]() 5+7=12+4
5+7=12+4![]() ,故②不正确;③正确;
,故②不正确;③正确;
综上可知正确的为①③④.
故答案为①③④.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案