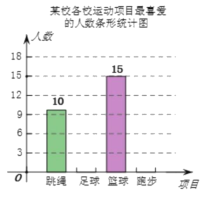
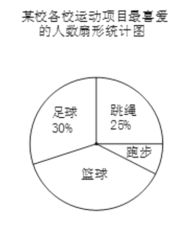
题目内容
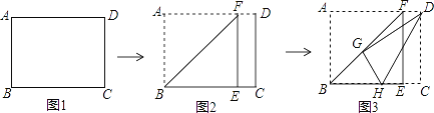
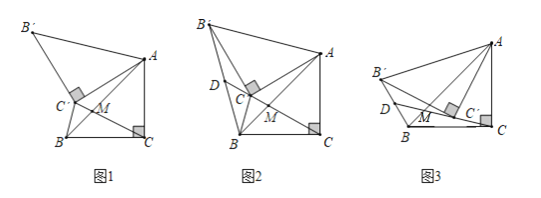
【题目】在△ABC中,∠ACB=90°,BC=AC=2,将△ABC绕点A顺时针方向旋转α角(0°<α<180°)至△AB'C'的位置.
问题探究:
(1)如图1,当旋转角为60°时,连接C'C与AB交于点M,则C'C= ,![]() .
.
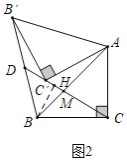
(2)如图2,在(1)条件下,连接BB',延长CC'交BB'于点D,求CD的长.
问题解决:
(3)如图3,在旋转的过程中,连线CC'、BB',CC'所在直线交BB'于点D,那么CD的长有没有最大值?如果有,求出CD的最大值:如果没有,请说明理由.
【答案】(1)2,2![]() ﹣2;(2)1+
﹣2;(2)1+![]() ;(3)
;(3)![]() 的长有最大值, 2
的长有最大值, 2![]() .
.
【解析】
(1)如图1中,证明![]() 是等边三角形即可解决问题.作
是等边三角形即可解决问题.作![]() 于
于![]() ,设
,设![]() ,构建方程求出
,构建方程求出![]() ,再根据
,再根据![]() 即可求出
即可求出![]() .
.
(2)如图2中,作![]() 于
于![]() .想办法证明
.想办法证明![]() ,
,![]() ,即可解决问题.
,即可解决问题.
(3)![]() 的值有最大值.取
的值有最大值.取![]() 的中点
的中点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,连接
,连接![]() .说明点
.说明点![]() 的运动轨迹是
的运动轨迹是![]() ,即可解决问题.
,即可解决问题.
解:(1)如图1中,作![]() 于
于![]() .
.
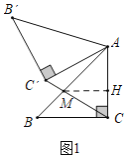
当旋转角为![]() 时,
时,![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
故答案为2,![]() .
.
(2)如图2中,作![]() 于
于![]() .
.
![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
(3)![]() 的长有最大值.
的长有最大值.
理由:如图3中,
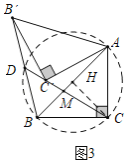
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() △
△![]() △
△![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
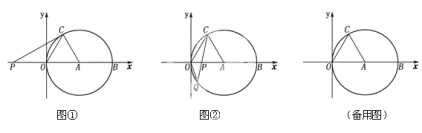
取![]() 的中点
的中点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,连接
,连接![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() 的运动轨迹是
的运动轨迹是![]() ,当
,当![]() 时,
时,![]() 的值最大,此时
的值最大,此时![]() .
.

练习册系列答案
相关题目