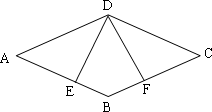
题目内容
如图,已知四边形ABCD是平行四边形,∠BCD的平分线CF交边AB于F,∠ADC的平分线DG交边AB于G.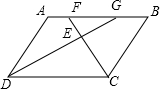
(1)求证:AF=BG;
(2)求证:△EFG为直角三角形;
(3)请你在已知条件的基础上再添加一个条件,使得△EFG为等腰直角三角形,并说明理由.
分析:(1)由角平分线知∠ADG=∠CDG,由平行知∠CDG=∠AGD所以,∠ADG=∠AGD,即AD=AG,同理BF=BC,又AD=BC,所以AG=BF,去掉公共部分,则有AF=GB;
(2)由于DG、CF是平行四边形一组邻角的平分线,所以可以证明△EFG是直角三角形.
(3)要使得△EFG成为等腰直角三角形,则必须有EF=EG或者∠EFG=∠EGF即可.
(2)由于DG、CF是平行四边形一组邻角的平分线,所以可以证明△EFG是直角三角形.
(3)要使得△EFG成为等腰直角三角形,则必须有EF=EG或者∠EFG=∠EGF即可.
解答:解:在平行四边形ABCD中
∵AD∥BC,AB=CD,
∴∠ADG=∠CDG,
又∵∠AGD=∠CDG,
∴∠ADG=∠AGD,
∴AD=AG.
同理BF=BC,
∴BF=AG,
即AF=BG;(5分)
(2)∵∠CDG=
,
∠ADC=∠DCF=
∠BCD,
而∠ADC+∠BCD=180°,
∴∠CDG+∠DCF=90°,
∴∠FEG=∠CED=90°,
即△GEF是直角三角形;(9分)
(3)当平行四边形ABCD是矩形时,△GEF是等腰直角三角形,
∵∠DCF=∠CDG=45°,
∴∠EFG=∠EGF=45°,
∴△GEF是等腰直角三角形.(12分)
∵AD∥BC,AB=CD,
∴∠ADG=∠CDG,
又∵∠AGD=∠CDG,
∴∠ADG=∠AGD,
∴AD=AG.
同理BF=BC,
∴BF=AG,
即AF=BG;(5分)
(2)∵∠CDG=
| 1 |
| 2 |
∠ADC=∠DCF=
| 1 |
| 2 |
而∠ADC+∠BCD=180°,
∴∠CDG+∠DCF=90°,
∴∠FEG=∠CED=90°,
即△GEF是直角三角形;(9分)
(3)当平行四边形ABCD是矩形时,△GEF是等腰直角三角形,
∵∠DCF=∠CDG=45°,
∴∠EFG=∠EGF=45°,
∴△GEF是等腰直角三角形.(12分)
点评:此题考查了平行四边形的基本性质,以及直角三角形的判定,难易程度适中.

练习册系列答案
相关题目
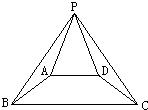 15、如图,已知四边形ABCD是等腰梯形,AB=DC,AD∥BC,PB=PC.求证:PA=PD.
15、如图,已知四边形ABCD是等腰梯形,AB=DC,AD∥BC,PB=PC.求证:PA=PD.
 的延长线分别交于点F、E,且
的延长线分别交于点F、E,且 (2013•梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
(2013•梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.