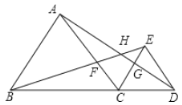
题目内容
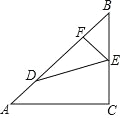
【题目】已知：如图，DE⊥AC，垂足为点E，∠AGF＝∠ABC，∠BFG+∠BDE＝180°，
求证：BF⊥AC．
请完成下面的证明的过程，并在括号内注明理由．
证明：∵∠AGF＝∠ABC（已知）
∴FG∥ （ ）
∴∠BFG＝∠FBC（ ）
∵∠BFG+∠BDE＝180°（已知）
∴∠FBC+∠BDE＝180°（ ）
∴BF∥DE（ ）
∴∠BFA＝ （两直线平行，同位角相等）
∵DE⊥AC（已知）
∴∠DEA＝90°（ ）
∴∠BFA＝90°（等量代换）
∴BF⊥AC（垂直的定义）
【答案】BC，同位角相等，两直线平行，两直线平行，内错角相等，等量代换，同旁内角互补，两直线平行，∠DEA，垂直的定义．
【解析】
先根据
得出
，故可得出
，由
可得出
，据此可得出结论．
解：∵∠AGF＝∠ABC（已知）
∴FG∥BC（同位角相等，两直线平行）
∴∠BFG＝∠FBC（两直线平行，内错角相等）
∵∠BFG+∠BDE＝180°（已知）
∴∠FBC+∠BDE＝180°（等量代换）
∴BF∥DE（同旁内角互补，两直线平行）
∴∠BFA＝∠DEA（两直线平行，同位角相等）
∵DE⊥AC（已知）
∴∠DEA＝90°（垂直的定义）
∴∠BFA＝90°（等量代换）
∴BF⊥AC（垂直的定义）.
故答案为：
，同位角相等，两直线平行，两直线平行，内错角相等，等量代换，同旁内角互补，两直线平行，
，垂直的定义．
【题目】在水果销售旺季，某水果店购进一优质水果，进价为20元/千克，售价不低于20元/千克，且不超过32元/千克，根据销售情况，发现该水果一天的销售量y（千克）与该天的售价x（元/千克）满足如下表所示的一次函数关系．
销售量y（千克） | … | 34.8 | 32 | 29.6 | 28 | … |
售价x（元/千克） | … | 22.6 | 24 | 25.2 | 26 | … |
（1）某天这种水果的售价为23.5元/千克，求当天该水果的销售量．
（2）如果某天销售这种水果获利150元，那么该天水果的售价为多少元？
