题目内容
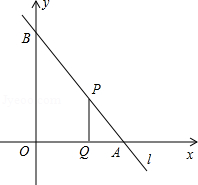
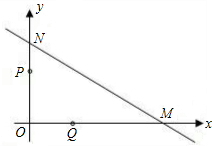
如图,直线l与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程x2﹣14x+4(AB+2)=0的两个根(OB>OA),P是直线l上A、B两点之间的一动点(不与A、B重合),PQ∥OB交OA于点Q【小题1】求tan∠BAO的值
【小题2】若S△PAQ=
 S四边形OQPB时,请确定点P在AB上的位置,并求出线段PQ的长;
S四边形OQPB时,请确定点P在AB上的位置,并求出线段PQ的长;【小题3】当点P在线段AB上运动时,在y轴上是否存在点M,使△MPQ为等腰直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【小题1】由已知可得
 ,
,又∵OA2+OB2=AB2,
∴(OA+OB)2﹣2OA•OB=AB2,
即142﹣8(AB+2)=AB2,
∴AB2+8AB﹣180=0,
∴AB=10或AB=﹣18(不合题意,舍去),
∴AB=10,
∴x2﹣14x+48=0,
解得x1=6,x2=8,
∵OB>OA,∴OA=6,OB=8,
∴tan∠BAO=
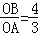 . (5分)
. (5分)【小题2】∵S△PAQ=
 S四边形OQPB,
S四边形OQPB,∴S△PAQ=
 S△AOB,
S△AOB,∵PQ∥BO,
∴△PQA∽△BOA,
∴
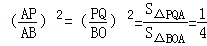 ,
,∴
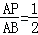 .∵AB=10,
.∵AB=10,∴AP=5,
又∵tan∠BAO=
 ,
,∴sin∠BAO=
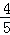 ,
,∴PQ=PA•sin∠BAO=
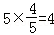 .(5分)
.(5分)【小题3】存在,
M点的坐标分别为M1(0,0)、M2(0,
 )、M3(0,
)、M3(0,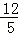 ).(2分)解析:
).(2分)解析:(1)根据勾股定理得出OA2+OB2=AB2,求出AB.然后把AB代入等式求出x的值继而求出OA,OB的值即可;
(2)已知S△PAQ=
 S四边形OQPB,证明△PQA∽△BOA利用线段比求出AB,AP的值.知道PQ=PA•sin∠BAO,即可求解.
S四边形OQPB,证明△PQA∽△BOA利用线段比求出AB,AP的值.知道PQ=PA•sin∠BAO,即可求解. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
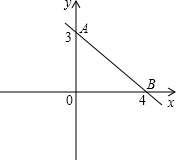 如图,直线m与x轴、y轴分别交于点B,A,且A,B两点的坐标分别为A(0,3),B(4,0).
如图,直线m与x轴、y轴分别交于点B,A,且A,B两点的坐标分别为A(0,3),B(4,0).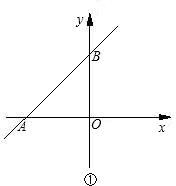
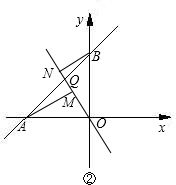
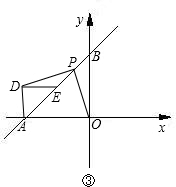
 点同时停止运动,设运动时间为t秒.
点同时停止运动,设运动时间为t秒. 已知:如图,直线AB与x轴交于点A,与y轴交于点B.
已知:如图,直线AB与x轴交于点A,与y轴交于点B.