题目内容
如图,直线l与x轴、y轴分别交于点M(8,0),点N(0,6).点P从点N出发,以每秒1个单位长度的速度沿N?O方向运动,点Q从点O出发,以每秒2个单位长度的速度沿O→M的方向运动.已知点P、Q同时出发,当点Q达点M时,P、Q两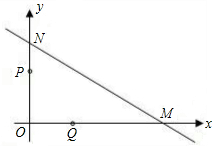 点同时停止运动,设运动时间为t秒.
点同时停止运动,设运动时间为t秒.(1)设四边形MNPQ的面积为S,求S关于t的函数关系式,并写出t的取值范围.
(2)当t为何值时,PQ与l平行.
分析:(1)由于四边形PQMN的形状不确定,因此可用△OMN的面积减去△OPQ的面积来求.△OMN的面积不难求出,而△OPQ中,可根据P、Q的速度,用时间t表示出OP,PQ的长,然后根据三角形的面积计算公式即可求出△OPQ的面积.由此可得出四边形的面积S与t的函数关系式.t的取值范围可根据Q与O,M两点不重合(重合时不能得出四边形PQMN)来求出.
(2)当PQ∥MN时,△OPQ∽△ONM,那么可得出关于OP,ON,OQ,OM的比例关系式.用t表示出OP、OQ后,可根据比例关系式求出t的值.
(2)当PQ∥MN时,△OPQ∽△ONM,那么可得出关于OP,ON,OQ,OM的比例关系式.用t表示出OP、OQ后,可根据比例关系式求出t的值.
解答:解:(1)依题意,运动总时间为t=
=4秒,要形成四边形MNPQ,则运动时间为0<t<4.(1分)
当P点在线段NO上运动t秒时,
OP=6-t,OQ=2t
∴S△POQ=
OP•OQ=-t2+6t
此时四边形MNPQ的面积
S=S△MON-S△POQ
=
×8×6-(-t2+6t)
=t2-6t+24
∴S关于t的函数关系式为S=t2-6t+24.(0<t<4)
(2)当PQ与l平行时,△NOM∽△POQ
=
即
=
∴10t=24,即t=2.4
∴当t=2.4秒时,PQ与l平行.
| 8 |
| 2 |
当P点在线段NO上运动t秒时,
OP=6-t,OQ=2t
∴S△POQ=
| 1 |
| 2 |
此时四边形MNPQ的面积
S=S△MON-S△POQ
=
| 1 |
| 2 |
=t2-6t+24
∴S关于t的函数关系式为S=t2-6t+24.(0<t<4)
(2)当PQ与l平行时,△NOM∽△POQ
| MO |
| QO |
| NO |
| PO |
| 8 |
| 2t |
| 6 |
| 6-t |
∴10t=24,即t=2.4
∴当t=2.4秒时,PQ与l平行.
点评:本题主要考查了梯形的性质,相似三角形的性质以及二次函数的应用等知识点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
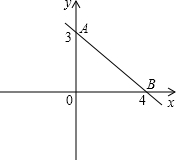 如图,直线m与x轴、y轴分别交于点B,A,且A,B两点的坐标分别为A(0,3),B(4,0).
如图,直线m与x轴、y轴分别交于点B,A,且A,B两点的坐标分别为A(0,3),B(4,0).

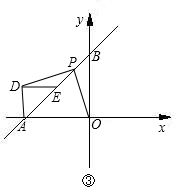
 已知:如图,直线AB与x轴交于点A,与y轴交于点B.
已知:如图,直线AB与x轴交于点A,与y轴交于点B.