题目内容
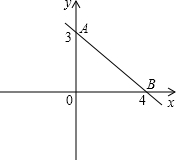 如图,直线m与x轴、y轴分别交于点B,A,且A,B两点的坐标分别为A(0,3),B(4,0).
如图,直线m与x轴、y轴分别交于点B,A,且A,B两点的坐标分别为A(0,3),B(4,0).(1)请求出直线m的函数解析式;
(2)在x轴上是否存在这样的点C,使△ABC为等腰三角形?请求出点C的坐标(不需要具体过程),并在坐标系中标出点C的大致位置.
分析:(1)根据待定系数法就代入坐标即可求出函数的解析式;
(2)根据等腰三角形的性质,可设C点坐标为(x,0),
当以AB为底时,可得AC=BC,即
=4-x,解得x=
;
当以BC为底时,可得AC=AB,即
=5,即得x=-4(当x=4时为点B);
当以AC为底时,可得AB=BC,即得x-4=5或4-x=5,即得x=9或-1;
(2)根据等腰三角形的性质,可设C点坐标为(x,0),
当以AB为底时,可得AC=BC,即
| x2+9 |
| 7 |
| 8 |
当以BC为底时,可得AC=AB,即
| x2+9 |
当以AC为底时,可得AB=BC,即得x-4=5或4-x=5,即得x=9或-1;
解答:解:(1)设直线m的函数解析式为y=kx+b;(1分)
分别把A(0,3),B(4,0)代入上式得:
b=3,0=4k+b(1分)
解得k=-
,b=3(1分)
∴所求直线m的函数解析式为y=k=-
x+3;(1分)
(2)根据等腰三角形的性质可得:
分别以AB,AC,BC为底,在x轴上存在四个这样的点C,他们的坐标分别是(
,0),(-1,0),(9,0),(-4,0).图上标明略(共4分)
分别把A(0,3),B(4,0)代入上式得:
b=3,0=4k+b(1分)
解得k=-
| 3 |
| 4 |
∴所求直线m的函数解析式为y=k=-
| 3 |
| 4 |
(2)根据等腰三角形的性质可得:
分别以AB,AC,BC为底,在x轴上存在四个这样的点C,他们的坐标分别是(
| 7 |
| 8 |
点评:用待定系数法确定函数的解析式,是常用的一种解题方法,要注意熟练掌握.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目


 点同时停止运动,设运动时间为t秒.
点同时停止运动,设运动时间为t秒. 已知:如图,直线AB与x轴交于点A,与y轴交于点B.
已知:如图,直线AB与x轴交于点A,与y轴交于点B.