题目内容
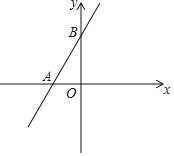
【题目】已知直线AB的函数表达式为y=![]() x+4,交x轴于点A,交y轴于点B,动点C从点A出发,以每秒2个单位长度的速度沿x轴正方向运动,设运动时间为t秒.
x+4,交x轴于点A,交y轴于点B,动点C从点A出发,以每秒2个单位长度的速度沿x轴正方向运动,设运动时间为t秒.
(1)求点A、B两点的坐标;
(2)当t为何值时,经过B、C两点的直线与直线AB关于y轴对称?并求出直线BC的函数关系式;
(3)在第(2)问的前提下,在直线AB上是否存在一点P,使得S△BCP=2S△ABC?如果存在,请求出此时点P的坐标;如果不存在,请说明理由.
【答案】(1)B(0,4),A(﹣3,0);(2)t=3秒,直线BC解析式为:y=﹣![]() x+4;(3)见解析.
x+4;(3)见解析.
【解析】
(1)令=0,则y=4可求出点B的坐标,令y=0,则0=![]() x+4可求得点A的坐标;
x+4可求得点A的坐标;
(2)先求出点A′的坐标,即点C的坐标,运用待定系数法可得直线BC的解析式;
(3)分两种情况:当点P在第三象限时,当点P在第一象限时分别求解即可.
(1)令=0,则y=4,
则点B(0,4),
令y=0,则0=![]() x+4,解得:x=﹣3,
x+4,解得:x=﹣3,
则点A(﹣3,0).
(2)点A关于y轴点对称点为A′(3,0),
所以当点C运动到A′(3,0)时,直线BC与直线AB关于y轴对称,则t=![]() =3秒.
=3秒.
设此时直线BC的解析式为:y=kx+b.
把点C(3,0)和点B(0,4)代入得:![]() ,
,
解得: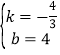 .
.
故直线BC解析式为:y=﹣![]() x+4.
x+4.
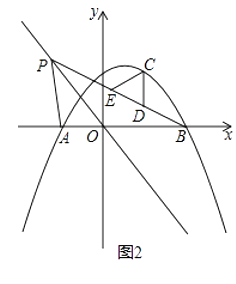
(3)存在,如图,当点P在第三象限时,S△BCP=2S△ABC,则S△ACP=S△ABC,
∴点P到x轴的距离等于点B到x轴的距离,
∴点P的纵坐标为﹣4,
把y=﹣4代入到y=![]() x+4中得:﹣4=
x+4中得:﹣4=![]() x+4,
x+4,
解得:x=﹣6,
则P(﹣6,﹣4);
当点P在第一象限时,S△BCP=2S△ABC,则S△ACP=3S△ABC,
∴点P到x轴的距离等于点B到x轴的距离,
∴点P的纵坐标为12,
把y=12代入到y=![]() x+4中得:12=
x+4中得:12=![]() x+4,
x+4,
解得:x=6,
则P'(6,12),
即:点P的坐标为(﹣6,﹣4)或(6,12).


 阅读快车系列答案
阅读快车系列答案【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?