题目内容
如图，PAB、PCD为⊙O的两条割线，AD、BC相交于点E，则图中相似三角形共有（ ）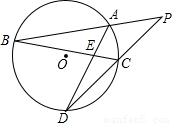
A．0对
B．1对
C．2对
D．3对
【答案】分析：找图中的相似三角形，根据相似三角形的判定方法，有两组对应角相等的三角形相似，因而解决的关键是找出图中相等的角．根据同弧所对的圆周角相等，因而有∠BAD=∠BCD，∠B=∠D，从而不难找到相似三角形．
解答：解：∵∠BEA=∠DEC，∠B=∠D
∴△ABE∽△CDE
∵∠BAD=∠BCD，∠P=∠P
∴△PBC∽△PDA
∴共有两对相似三角形
故选C
点评：在圆中找相等的角，依据是同弧或等弧所对的圆周角相等或圆心角相等，再根据相似三角形的判定即可得到．
解答：解：∵∠BEA=∠DEC，∠B=∠D
∴△ABE∽△CDE
∵∠BAD=∠BCD，∠P=∠P
∴△PBC∽△PDA
∴共有两对相似三角形
故选C
点评：在圆中找相等的角，依据是同弧或等弧所对的圆周角相等或圆心角相等，再根据相似三角形的判定即可得到．
练习册系列答案
相关题目
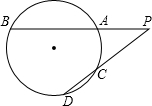如图，PAB、PCD是⊙O的两条割线，PA=3，AB=5，PC=4，则CD等于（ ）| A、6 | ||
| B、2 | ||
C、
| ||
D、
|
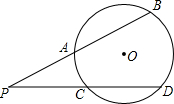如图，PAB、PCD是⊙O的割线，PA=3，PB=6，PC=2，则PD=
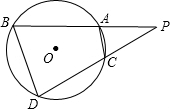如图，PAB、PCD为⊙O的两条割线，若PA=5，AB=7，CD=11，则AC：BD=
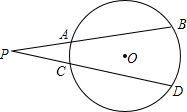如图，PAB和PCD是⊙O的两条割线，弧AC度数为20°，弧BD度数为60°，则∠P=
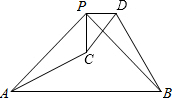（2012•新化县二模）如图，△PAB与△PCD都是等腰直角三角形，∠APB=∠CPD=90°，连接AC、BD，试猜想线段AC和BD的数量关系，并证明你的猜想．