题目内容
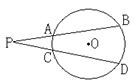
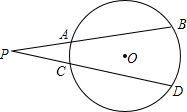 如图,PAB和PCD是⊙O的两条割线,弧AC度数为20°,弧BD度数为60°,则∠P=
如图,PAB和PCD是⊙O的两条割线,弧AC度数为20°,弧BD度数为60°,则∠P=20°
20°
.分析:首先连接OA,OB,OC,OD,由弧AC度数为20°,弧BD度数为60°,可得∠AOC=20°,∠BOD=60°,又由等腰三角形的性质,即可求得∠BAO+∠DCO的度数,继而求得答案.
解答: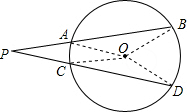 解:连接OA,OB,OC,OD,
解:连接OA,OB,OC,OD,
∵弧AC度数为20°,弧BD度数为60°,
∴∠AOC=20°,∠BOD=60°,
∴∠AOB+∠COD=360°-20°-60°=280°,
∵OA=OB,OC=OD,
∴∠BAO=
,∠DCO=
,
∴∠BAO+∠DCO=180°-
(∠AOB+∠COD)=180°-
×280°=40°,
∴∠PAO+∠PCO=360°-(∠BAO+∠DCO)=320°,
∴∠P=360°-∠PAO-∠PCO-∠AOC=360°-320°-20°=20°.
故答案为:20°.
 解:连接OA,OB,OC,OD,
解:连接OA,OB,OC,OD,∵弧AC度数为20°,弧BD度数为60°,
∴∠AOC=20°,∠BOD=60°,
∴∠AOB+∠COD=360°-20°-60°=280°,
∵OA=OB,OC=OD,
∴∠BAO=
| 180°-∠AOB |
| 2 |
| 180°-∠COD |
| 2 |
∴∠BAO+∠DCO=180°-
| 1 |
| 2 |
| 1 |
| 2 |
∴∠PAO+∠PCO=360°-(∠BAO+∠DCO)=320°,
∴∠P=360°-∠PAO-∠PCO-∠AOC=360°-320°-20°=20°.
故答案为:20°.
点评:此题考查了弧、圆心角的性质、等腰三角形的性质以及四边形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 ,弧BD度数为
,弧BD度数为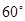 ,则∠P=
,则∠P=
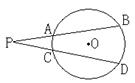
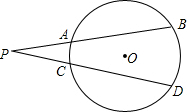 如图,PAB和PCD是⊙O的两条割线,弧AC度数为20°,弧BD度数为60°,则∠P=________.
如图,PAB和PCD是⊙O的两条割线,弧AC度数为20°,弧BD度数为60°,则∠P=________.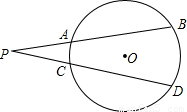
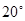 ,弧BD度数为
,弧BD度数为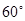 ,则∠P=
,则∠P=