题目内容
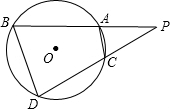如图，PAB、PCD为⊙O的两条割线，若PA=5，AB=7，CD=11，则AC：BD=分析：根据切割线定理可以求得∠D=∠PAC，即可求证△PAC∽△PDB，根据对应边比值相等的性质和CD的长可求得PC与PB的比值，即可解题．
解答：解：∵PAB、PCD为⊙O的两条割线，
∴∠BAC+∠BDC=180°，∠PAC+∠BAC=180°，
∴∠BDC=∠PAC，又∵∠P=∠P，
∴△PAC∽△PDB，∴
=
，
设PC=x，PD=y，且y-x=11，
解得x=4，y=15，
∴
=
=
=
，
故答案为
．
∴∠BAC+∠BDC=180°，∠PAC+∠BAC=180°，
∴∠BDC=∠PAC，又∵∠P=∠P，
∴△PAC∽△PDB，∴
| PA |
| PD |
| PC |
| PB |
设PC=x，PD=y，且y-x=11，
解得x=4，y=15，
∴
| AC |
| BD |
| PC |
| PB |
| 4 |
| 12 |
| 1 |
| 3 |
故答案为
| 1 |
| 3 |
点评：本题考查了相似三角形的判定，考查了切割线定理，考查了相似三角形对应边比值相等的性质，本题中根据CD和对应边比值相等的性质求AC：BD的值是解题的关键．
练习册系列答案
相关题目
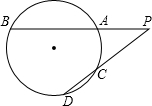如图，PAB、PCD是⊙O的两条割线，PA=3，AB=5，PC=4，则CD等于（ ）| A、6 | ||
| B、2 | ||
C、
| ||
D、
|
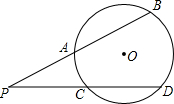如图，PAB、PCD是⊙O的割线，PA=3，PB=6，PC=2，则PD=
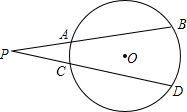如图，PAB和PCD是⊙O的两条割线，弧AC度数为20°，弧BD度数为60°，则∠P=
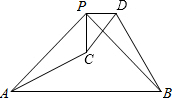（2012•新化县二模）如图，△PAB与△PCD都是等腰直角三角形，∠APB=∠CPD=90°，连接AC、BD，试猜想线段AC和BD的数量关系，并证明你的猜想．