��Ŀ����
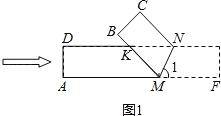
����Ŀ����ѧ�о����ϣ���ʦ������̽������ֽ�е���ѧ���⡷ʱ����ʾ��ͼ1��ʾ�ij�����ֽ��![]() ������
������![]() ��
��![]() ��Ȼ����ֽ�������⻭һ�����߶�
��Ȼ����ֽ�������⻭һ�����߶�![]() ����ֽƬ��
����ֽƬ��![]() �۵���
�۵���![]() ��
��![]() ���ڵ�
���ڵ�![]() ���õ�
���õ�![]() ����ͼ2��ʾ��
����ͼ2��ʾ��

̽����
��1����![]() ��
��![]() ______�㣻
______�㣻
��2���ı��ۺ�![]() λ�ã�
λ�ã�![]() ʼ����______�����Σ���˵�����ɣ�
ʼ����______�����Σ���˵�����ɣ�
Ӧ�ã�
��3�������Խ��С�����о�![]() �����ʱ������
�����ʱ������![]() ���ϵĸ�ʼ���Ǹ������ֵ��������һ���֣����ܿ��о���
���ϵĸ�ʼ���Ǹ������ֵ��������һ���֣����ܿ��о���![]() �������СֵΪ
�������СֵΪ![]() ����ʱ
����ʱ![]() �Ĵ�С����Ϊ______�㣻
�Ĵ�С����Ϊ______�㣻
��4��С���������ֲ�����������![]() ��������ֵ���������������ֵ��
��������ֵ���������������ֵ��
���𰸡���1��![]() ����2��������֤�������������3��
����2��������֤�������������3��![]() ��
��![]() ����4��
����4��![]() ��������ֵΪ
��������ֵΪ![]()
��������
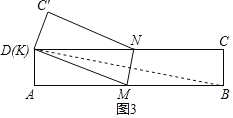
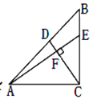
��1�����ݾ��ε����ʺ��۵������������KNM����KMN�Ķ����������������ڽǺͼ�����⣻
��2�����÷��۱任�������Լ���ֱ��ƽ���ڴ�����ȵó�KM=KN��
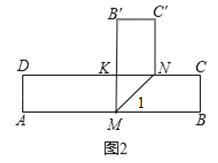
��3��������������ۣ�����ͼ2�����õ���KMN�������СֵΪ![]() ʱ��KN=BC=1����KN��B'M���ó���1=��NMB=45�㣻����ͼ2��2��������KMN�������СֵΪ
ʱ��KN=BC=1����KN��B'M���ó���1=��NMB=45�㣻����ͼ2��2��������KMN�������СֵΪ![]() ʱ��KN=KM=BC=1����KM��B'M�����۵������ʺ��ܽǵĶ��弴�ɵó����ۣ�
ʱ��KN=KM=BC=1����KM��B'M�����۵������ʺ��ܽǵĶ��弴�ɵó����ۣ�
��4�������һ��������ֽƬ���ۣ�ʹ��B��D�غϣ���ʱ��KҲ��D�غϣ��������������ֽƬ�ضԽ���AC���ۣ���ʱ�ۺۼ�ΪAC�������������⣮
��1����ͼ1��
���ı���ABCD�Ǿ��Σ���AM��DN�����KNM=��1��
�ߡ�1=70�㣬���KNM=��KMN=��1=70�㣬���MKN=40�㣮
�ʴ�Ϊ��40��
��2���������������£�
��AB��CD�����1=��MND��
�߽�ֽƬ��MN�۵������1=��KMN�����MND=��KMN����KM=KN��
�ʴ�Ϊ��������
��3��������������ۣ�����ͼ2������KMN�������СֵΪ![]() ʱ��KN=BC=1����KN��B'M��
ʱ��KN=BC=1����KN��B'M��
�ߡ�NMB=��KMN����KMB=90�㣬���1=��NMB=45�㣮
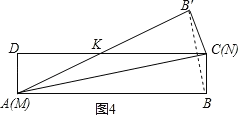
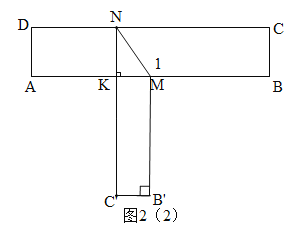
����ͼ2��2��������KMN�������СֵΪ![]() ʱ��KN=KM=BC=1����KM��B'M��
ʱ��KN=KM=BC=1����KM��B'M��
�ߡ�NMB=��NMB'����BMB'=90�㣬���1=��NMB=��360�㣭90�㣩��2=135�㣮
�ʴ�Ϊ��45���135�㣻
��4�������������
���һ����ͼ3��������ֽƬ���ۣ�ʹ��B��D�غϣ���ʱ��KҲ��D�غϣ�
MK=MB=x����AM=5��x��
�ɹ��ɶ����ã�12+��5��x��2=x2��
��ã�x=2.6����MD=ND=2.6��
S��MNK=S��MND![]() 1��2.6=1.3��
1��2.6=1.3��
���������ͼ4��������ֽƬ�ضԽ���AC���ۣ���ʱ�ۺۼ�ΪAC��
MK=AK=CK=x����DK=5��x��
ͬ���ɵã�MK=NK=2.6��
��MD=1����S��MNK![]() 1��2.6=1.3��
1��2.6=1.3��
��MNK��������ֵΪ1.3��