题目内容
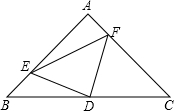 已知在△ABC中,∠A=90°,AB=AC,D为BC的中点.
已知在△ABC中,∠A=90°,AB=AC,D为BC的中点.(1)如图,E、F分别是AB,AC上的动点,且BE=AF,求证:△DEF为等腰直角三角形;
(2)在(1)的条件下,四边形AEDF的面积是否变化,证明你的结论;
(3)若E、F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论.
分析:(1)题要通过构建全等三角形来求解.连接AD,可通过证△ADF和△BDE全等来求本题的结论.
(2)题可把将四边形AEDF的面积分成△ADF和ADE的面积和求解,由(1)证得△ADF和△BDE全等,因此四边形AEDF的面积可转化为△ABD的面积,由此得证.
(3)与(1)题的思路和解法一样.
(2)题可把将四边形AEDF的面积分成△ADF和ADE的面积和求解,由(1)证得△ADF和△BDE全等,因此四边形AEDF的面积可转化为△ABD的面积,由此得证.
(3)与(1)题的思路和解法一样.
解答: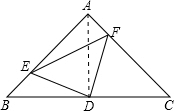 (1)证明:连接AD
(1)证明:连接AD
∵AB=AC,∠A=90°,D为BC中点
∴AD=
=BD=CD
且AD平分∠BAC
∴∠BAD=∠CAD=45°
在△BDE和△ADF中,
∴△BDE≌△ADF(SAS)
∴DE=DF,∠BDE=∠ADF
∵∠BDE+∠ADE=90°
∴∠ADF+∠ADE=90°
即:∠EDF=90°
∴△EDF为等腰直角三角形.
(2)解:四边形AEDF面积不变.
理由:∵由(1)可知,△AFD≌△BED
∴S△BDE=S△ADF,
而S四边形AEDF=S△AED+S△ADF=S△AED+S△BDE=S△ABD
∴S四边形AEDF不会发生变化.
(3)解:仍为等腰直角三角形.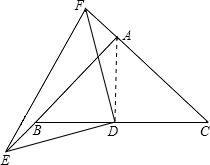
理由:∵△AFD≌△BED
∴DF=DE,∠ADF=∠BDE
∵∠ADF+∠FDB=90°
∴∠BDE+∠FDB=90°
即:∠EDF=90°
∴△EDF为等腰直角三角形.
 (1)证明:连接AD
(1)证明:连接AD∵AB=AC,∠A=90°,D为BC中点
∴AD=
| BC |
| 2 |
且AD平分∠BAC
∴∠BAD=∠CAD=45°
在△BDE和△ADF中,
|
∴△BDE≌△ADF(SAS)
∴DE=DF,∠BDE=∠ADF
∵∠BDE+∠ADE=90°
∴∠ADF+∠ADE=90°
即:∠EDF=90°
∴△EDF为等腰直角三角形.
(2)解:四边形AEDF面积不变.
理由:∵由(1)可知,△AFD≌△BED
∴S△BDE=S△ADF,
而S四边形AEDF=S△AED+S△ADF=S△AED+S△BDE=S△ABD
∴S四边形AEDF不会发生变化.
(3)解:仍为等腰直角三角形.

理由:∵△AFD≌△BED
∴DF=DE,∠ADF=∠BDE
∵∠ADF+∠FDB=90°
∴∠BDE+∠FDB=90°
即:∠EDF=90°
∴△EDF为等腰直角三角形.
点评:本题综合考查了等腰三角形的性质及判定、全等三角形的判定和性质等知识,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.
22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.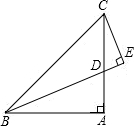 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC.
如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.