题目内容
【题目】如图,若AB∥CD,在下列三种情况下探究∠APC与∠PAB,∠PCD的数量关系.
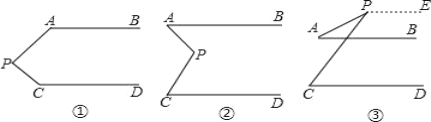
(1)图①中,∠APC+∠PAB+∠PCD= ;
(2)图②中, ;
(3)图③中,写出∠APC与∠PAB,∠PCD的三者数量关系,并说明理由
【答案】(1)360°
(2)∠APC=∠PAB+∠PCD
(3)∠APC+∠PAB=∠PCD,理由见解析.
【解析】试题分析:三个图形中过P作PE与AB平行,由AB与CD平行,利用平行于同一条直线的两直线平行得到PE与CD平行,利用平行线的性质判断即可得到结果.
试题解析:(1)过P作PE∥AB,如图①
∵AB∥CD,
∴PE∥CD,
∴∠A+∠APE=180°,∠EPC+∠C=180°,
∴∠APC+∠PAB+∠PCD=∠A+∠APE+∠EPC+∠C=360°;
(2)过P作PE∥AB,如图②
∵AB∥CD,
∴PE∥CD,
∴∠A=∠APE,∠EPC=∠C,
∴∠APC=∠APE+∠EPC=∠PAB+∠PCD;
(3)∠APC=∠PCD-∠PAB,
理由为:过P作PE∥AB,如图③
∵AB∥CD,
∴PE∥CD,
∴∠PAB+∠APE=180°,∠EPC+∠PCD=180°,
即∠APE=180°-∠PAB,∠EPC=180°-∠PCD,
∴∠APC=∠APE-∠EPC=∠PCD-∠PAB.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

