��Ŀ����
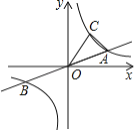
����Ŀ����ͼ��ֱ��l��������ֱ���A��B���㣬��BAO=45�㣬��A����Ϊ��8��0��������P�ӵ�O�����������߶�OBA�˶�������Aֹͣ��ͬʱ����QҲ�ӵ�O���������߶�OA�˶�������Aֹͣ�����ǵ��˶��ٶȾ�Ϊÿ��1����λ���ȣ�

��1����ֱ��AB�ĺ�����ϵʽ��
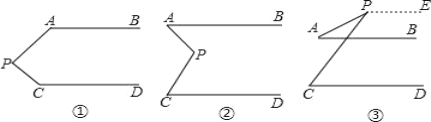
��2������A��B��O��ƽ���ڵ�E��ɵ�ͼ����ƽ���ı��Σ���ֱ��д����E�����ꣻ
��3�����˶������У���P��Q�ľ���Ϊ2ʱ�����P�����꣮
���𰸡���1��y=��x+8����2������������3��P�䣨8��![]() ��
��![]() ����
����
��������
�����������1����ֱ��AB����ʽΪy=kx+b����A��B����������k��b��ֵ������ȷ��������ʽ��
��2�����������������ͼ��ʾ���ı���AOBE1Ϊƽ���ı���ʱ���ı���ABE2OΪƽ���ı���ʱ���ı���ABOE3Ϊƽ���ı���ʱ���ֱ����E�����꼴�ɣ�
��3��������������ǣ���P��OB��ʱ������PQ������PQ�ij���������OPQΪ����ֱ�������Σ����OP�ij���ȷ������ʱP���ꣻ��P����AB��ʱ����P����P��M��x�ᣬȷ������ʱP�����꼴�ɣ�
�⣺��1���ߡ�BAO=45�㣬��AOB=90�㣬
���AOBΪ����ֱ�������Σ���OA=OB=8��
��B��0��8����
��ֱ��AB����ʽΪy=kx+b��
��A��8��0����B��0��8������ã�![]() ��
��
��ã�k=��1��b=8��
��ֱ��AB����ʽΪy=��x+8��
��2����ͼ��ʾ�����ı���AOBE1Ϊƽ���ı���ʱ��E1����Ϊ��8��8����
���ı���ABE2OΪƽ���ı���ʱ��E2����Ϊ����8��8����
���ı���ABOE3Ϊƽ���ı���ʱ��E3����Ϊ��8����8����
��3����P��OB��ʱ������PQ����PQ=2��
��Rt��POQ�У�OP=OQ���ɵã�OP=OQ=![]() ��2=
��2=![]() ����ʱP��0��
����ʱP��0��![]() ����
����
��P����AB��ʱ����P����P��M��x�ᣬ
��P��Q��=2����P��Q��MΪ����ֱ�������Σ�
��P��M=Q��M=![]() ��OM=OB��P��M=8��
��OM=OB��P��M=8��![]() ��
��
��ʱP�䣨8��![]() ��
��![]() ����
����
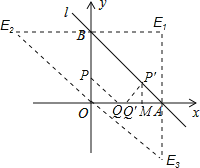

 ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�����Ŀ����ͼ1���ڡ�ABC�У�OB��OC�ǡ�ABC����ACB�Ľ�ƽ���ߣ�
��1����д����ı���
��A�Ķ��� | 50�� | 60�� | 70�� |
��BOC�Ķ��� |
��2���Բ����A���BOC֮�����һ��������������ϵ����֤����IJ��룻
��3����ͼ2����ABC�ĸ�BE��CD����O�㣬��˵��ͼ�С�A���BOD�Ĺ�ϵ��