题目内容
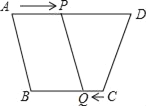
【题目】(1)用不同的方法计算如图中阴影部分的面积得到的等式: ;
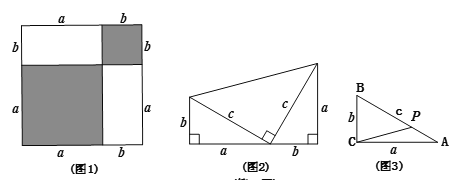
(2)如图是两个边长分别为![]() 、
、![]() 、
、![]() 的直角三角形和一个两条直角边都是
的直角三角形和一个两条直角边都是![]() 的直角三角形拼成,试用不同的方法计算这个图形的面积,你能发现什么?说明理由;
的直角三角形拼成,试用不同的方法计算这个图形的面积,你能发现什么?说明理由;
(3)根据上面两个结论,解决下面问题:若如图中,直角![]() 三边a、
三边a、![]() 、c,
、c,
①满足![]() ,ab=18,求
,ab=18,求![]() 的值;
的值;
②在①的条件下,若点![]() 是边
是边![]() 上的动点,连接
上的动点,连接![]() ,求线段
,求线段![]() 的最小值;
的最小值;
③若![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的值是 .
的值是 .
【答案】(1)![]() ,(2)
,(2)![]() ;(3)①
;(3)①![]() ,②
,②![]() ;③10.
;③10.
【解析】
(1)阴影部分的面积等于大阴影正方形的面积+小阴影正方形的面积,也等于大正方形的面积-两个长方形的面积;
(2)一种方法是根据梯形的面积公式计算,另一种方法是三个直角三角形的面积和;
(3)①利用完全平方公式的变形求出![]() 的值,再利用
的值,再利用![]() 即可求出
即可求出![]() 的值;②当
的值;②当![]() 是
是![]() 边上的高时,
边上的高时,![]() 的值最小,利用面积法求解即可;③根据题意得出a+b=12,ab=22,然后可求出c值.
的值最小,利用面积法求解即可;③根据题意得出a+b=12,ab=22,然后可求出c值.
解:(1)![]() ,
,
(2)![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
(3)①当 ![]() ,ab=18 时,
,ab=18 时,
![]()
![]()
![]() ,
,
因为![]() ,
,
所以![]() ,
,
所以![]() ,
,
② 当![]() 是
是![]() 边上的高时,
边上的高时,![]() 的值最小 (垂线段最短),
的值最小 (垂线段最短),
因为![]() ,
,
∴![]() ,
,
∴![]() ;
;
③∵![]() ,
,![]() ,且
,且![]() ,
,
∴a+b=12,ab=22,
∴![]() =144-44=100,
=144-44=100,
∴c2=100,
∴c=10.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目