题目内容

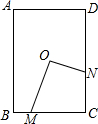精英家教网如图，O为矩形ABCD的中心，M为BC边上任一点，ON⊥OM且与CD边交于点N．若AB=6，AD=4，设OM=x，ON=y，则y与x的函数关系式为
 
．
分析：求两条线段的关系，把两条线段放到两个三角形中，利用两个三角形的关系求解．
解答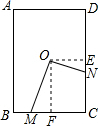：精英家教网解：如图，作OF⊥BC于F，OE⊥CD于E，
∵ABCD为矩形
∴∠C=90°
∵OF⊥BC，OE⊥CD
∴∠EOF=90°
∴∠EON+∠FON=90°
∵ON⊥OM
∴∠EON=∠FOM
∴△OEN∽△OFM
∴
OE
OF
=
ON
OM

∵O为中心
∴
OF
OE
=
AB
AD
=
6
4
=
3
2

∴
OM
ON
=
3
2

即y=
2
3
x
点评：此题主要考查的是合理的在图中作出辅助线，熟练掌握相似三角形的判定定理和性质．
练习册系列答案
相关题目
26、如图，在等边△ABC中，点D是BC边的中点，以AD为边作等边△ADE．
（1）求∠CAE的度数；
（2）取AB边的中点F，连接CF、CE，试证明四边形AFCE是矩形．
如图，等边三角形ABC，边长为2，AD是BC边上的高．
（1）在△ABC内部作一个矩形EFGH（如图1），其中E、H分别在边AB、AC上，FG在边BC上．
①设矩形的一边FG=x，那么EF=
 
．（用含有x的代数式表示）
②设矩形的面积为y，当x取何值时，y的值最大，最大值是多少？
（2）在图2中，只用圆规画出点E，使得上述矩形EFGH面积最大．写出画法，并保留作图痕迹．
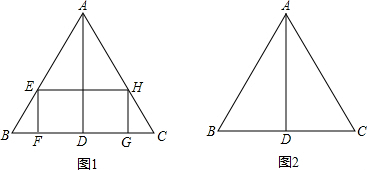
精英家教网
定义：只有一组对角是直角的四边形叫做损矩形，连接它的两个非直角顶点的线段叫做这个损矩形的直径．
（1）如图1，损矩形ABCD，∠ABC=∠ADC=90°，则该损矩形的直径是线段
 
．
（2）在线段AC上确定一点P，使损矩形的四个顶点都在以P为圆心的同一圆上（即损矩形的四个顶点在同一个圆上），请作出这个圆，并说明你的理由．友情提醒：“尺规作图”不要求写作法，但要保留作图痕迹．
（3）如图2，△ABC中，∠ABC=90°，以AC为一边向形外作菱形ACEF，D为菱形ACEF的中心，连接BD，当BD平分∠ABC时，判断四边形ACEF为何种特殊的四边形？请说明理由．若此时AB=3，BD=4
2
，求BC的长．
精英家教网精英家教网
如图，四边形DEFG是△ABC的内接矩形，如果△ABC的高线AH长8cm，底边BC长10cm，设DG=xcm，DE=ycm，则y关于x的函数关系式为
y=-
4
5
x+8
y=-
4
5
x+8
．
（1）如图1，在平行四边形ABCD中，E、F为BC上两点，且BE=CF，AF=DE．
求证：①△ABF≌△DCE；②四边形ABCD是矩形．
（2）如图2，已知△ABC是等边三角形，D点是AC的中点，延长BC到E，使CE=CD．
①请用尺规作图的方法，过点D作DM⊥BE，垂足为M；（不写作法，保留作图痕迹）
②求证：BM=EM．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网