题目内容
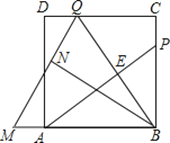
【题目】如图,P为正方形ABCD的边BC上一动点(P与B.C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.
(1)求证:AP⊥BQ;
(2)若AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长。
【答案】(1)证明见解析;(2)MQ=![]() ;(3)AM=
;(3)AM=![]() .
.
【解析】
试题(1)证明△ABP≌△BCQ,则∠BAP=∠CBQ,从而证明∠CBQ+∠APB=90°,进而得证;
(2)设MQ=MB=x,则MN=x﹣2.在直角△MBN中,利用勾股定理即可列方程求解;
(3)设AM=y,BN=BC=m+n,在直角△BNM中,MB=y+m+n,MN=MQ﹣QN=(y+m+n)﹣m=y+n,利用勾股定理即可求解.
试题解析:(1)证明:∵四边形ABCD是正方形,∴∠ABC=∠C=90°,AB=BC,在△ABP和△BCQ中,∵AB=BC,∠ABC=∠C,BP=CQ,∴△ABP≌△BCQ,∴∠BAP=∠CBQ.
∵∠BAP+∠APB=90°,∴∠CBQ+∠APB=90°,∴∠BEP=90°,∴AP⊥BQ;
(2)解:∵正方形ABCD中,AB=3,BP=2CP,∴BP=2,由(1)可得NQ=CQ=BP=2,NB=3.
又∵∠NQB=∠CQB=∠ABQ,∴MQ=MB.
设MQ=MB=x,则MN=x﹣2.
在直角△MBN中,![]() ,即
,即![]() ,解得:x=
,解得:x=![]() ,即MQ=
,即MQ=![]() ;
;
(3)∵BP=m,CP=n,由(1)(2)得MQ=BM,CQ=QN=BP=m,设AM=y,BN=BC=m+n,在直角△BNM中,MB=y+m+n,MN=MQ﹣QN=(y+m+n)﹣m=y+n,![]() ,即
,即![]() ,则y=
,则y=![]() ,AM=
,AM=![]() .
.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目