题目内容
【题目】已知正方形ABCD的边长为10,现改变该正方形的边长,使其变为矩形.若AD的长增加了x,AB的长减少了kx(其中k>0,x>0).
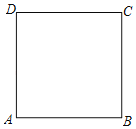
(1)若k=2,请说明改变后得到的矩形面积是否可为125;
(2)若改变后得到的矩形面积仍为100,求x与k的数量关系.
【答案】(1)改变后得到的矩形面积不能为125;(2)x=![]() .
.
【解析】
(1)根据矩形的面积公式结合改变后矩形的面积为125,即可得出关于x的一元二次方程,由根的判别式△=100<0,即可得出改变后得到的矩形面积不能为125;
(2)根据矩形的面积公式结合改变后矩形的面积为100,即可得出关于x的一元二次方程,由k>0,x>0,即可得出x与k的数量关系.
(1)依题意,得:(10+x)(10﹣2x)=125,
整理,得:2x2+10x+25=0.
∵△=102﹣4×2×25=﹣100<0,
∴改变后得到的矩形面积不能为125.
(2)依题意,得:(10+x)(10﹣kx)=100,
整理,得:kx2﹣(1﹣k)x=0.
∵k>0,x>0,
∴x=![]() .
.

 黄冈创优卷系列答案
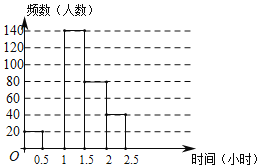
黄冈创优卷系列答案【题目】某区规定学生每天户外体育活动时间不少于1小时,为了解学生参加户外体育活动的情况,对部分学生每天参加户外体育活动的时间进行了随机抽样调查,并将调查结果绘制成如图的统计图表(不完整).请根据图表中的信息,解答下列问题:
(1)表中的a=_____,将频数分布直方图补全;
(2)该区8000名学生中,每天户外体育活动的时间不足1小时的学生大约有多少名?
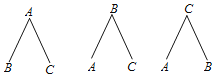
(3)若从参加户外体育活动时间最长的3名男生和1名女生中随机抽取两名,请用画树状图或列表法求恰好抽到1名男生和1名女生的概率.
组别 | 时间(小时) | 频数(人数) | 频率 |
A | 0≤t<0.5 | 20 | 0.05 |
B | 0.5≤t<1 | a | 0.3 |
C | l≤t<1.5 | 140 | 0.35 |
D | 1.5≤t<2 | 80 | 0.2 |
E | 2≤t<2.5 | 40 | 0.1 |