题目内容
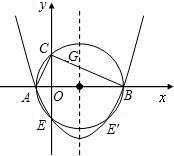 如图,在Rt△ABC中,∠ACB=90°,BC>AC,以斜边AB所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA2+OB2=17,且线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根.
如图,在Rt△ABC中,∠ACB=90°,BC>AC,以斜边AB所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA2+OB2=17,且线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根.(1)求C点的坐标;
(2)以斜边AB为直径作圆与y轴交于另一点E,求过A、B、E三点的抛物线的解析式,并画出此抛物线的草图;
(3)在抛物线上是否存在点P,使△ABP与△ABC全等?若存在,求出符合条件的P点的坐标;若不存在,说明理由.
分析:(1)线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根.根据韦达定理就可以得到关于OA,OB的两个式子,再已知OA2+OB2=17,就可以得到一个关于m的方程,从而求出m的值.求出OA,OB.根据OC2=OA•OB就可以求出C点的坐标;
(2)由第一问很容易求出A,B的坐标.连接AB的中点,设是M,与E,在直角△OME中,根据勾股定理就可以求出OE的长,得到E点的坐标,利用待定系数法就可以求出抛物线的解析式;
(3)E点就是满足条件的点.同时C,E关于抛物线的对称轴的对称点也是满足条件的点.
(2)由第一问很容易求出A,B的坐标.连接AB的中点,设是M,与E,在直角△OME中,根据勾股定理就可以求出OE的长,得到E点的坐标,利用待定系数法就可以求出抛物线的解析式;
(3)E点就是满足条件的点.同时C,E关于抛物线的对称轴的对称点也是满足条件的点.
解答:解:(1)∵线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根,
∴
又∵OA2+OB2=17,
∴(OA+OB)2-2•OA•OB=17,(3)
∴把(1)(2)代入(3),得m2-4(m-3)=17,
∴m2-4m-5=0,
解之,得m=-1或m=5,
又知OA+OB=m>0,
∴m=-1应舍去,
∴当m=5时,得方程x2-5x+4=0,
解之,得x=1或x=4,
∵BC>AC,
∴OB>OA,
∴OA=1,OB=4,
在Rt△ABC中,∠ACB=90°,CO⊥AB,
∴△AOC∽△COB,
∴OC2=OA•OB=1×4=4,
∴OC=2,
∴C(0,2);
(2)∵OA=1,OB=4,C、E两点关于x轴对称,
∴A(-1,0),B(4,0),E(0,-2),
设经过A、B、E三点的抛物线的解析式为y=ax2+bx+c,
则
解之,得
,
∴所求抛物线解析式为y=
x2-
x-2;
(3)存在,
∵点E是抛物线与圆的交点,
∴Rt△ACB≌RT△AEB,
∴E(0,-2)符合条件,
∵圆心的坐标(
,0)在抛物线的对称轴上,
∴这个圆和这条抛物线均关于抛物线的对称轴对称,
∴点E关于抛物线对称轴的对称点E′也符合题意,
∴可求得E′(3,-2),
∴抛物线上存在点P符合题意,它们的坐标是(0,-2)和(3,-2).
∴
|
又∵OA2+OB2=17,
∴(OA+OB)2-2•OA•OB=17,(3)
∴把(1)(2)代入(3),得m2-4(m-3)=17,
∴m2-4m-5=0,
解之,得m=-1或m=5,
又知OA+OB=m>0,
∴m=-1应舍去,
∴当m=5时,得方程x2-5x+4=0,
解之,得x=1或x=4,
∵BC>AC,
∴OB>OA,
∴OA=1,OB=4,
在Rt△ABC中,∠ACB=90°,CO⊥AB,
∴△AOC∽△COB,
∴OC2=OA•OB=1×4=4,
∴OC=2,
∴C(0,2);
(2)∵OA=1,OB=4,C、E两点关于x轴对称,
∴A(-1,0),B(4,0),E(0,-2),
设经过A、B、E三点的抛物线的解析式为y=ax2+bx+c,
则
|
|
∴所求抛物线解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(3)存在,
∵点E是抛物线与圆的交点,
∴Rt△ACB≌RT△AEB,
∴E(0,-2)符合条件,
∵圆心的坐标(
| 3 |
| 2 |
∴这个圆和这条抛物线均关于抛物线的对称轴对称,
∴点E关于抛物线对称轴的对称点E′也符合题意,
∴可求得E′(3,-2),
∴抛物线上存在点P符合题意,它们的坐标是(0,-2)和(3,-2).
点评:本题是二次函数与圆以及全等三角形相结合的题目,难度较大,利用数形结合有利于对题目的理解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F. 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离.
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离. 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直. 如图,在Rt△ABC中,BD⊥AC,sinA=
如图,在Rt△ABC中,BD⊥AC,sinA= 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).