Question

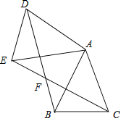
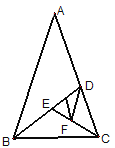
【题目】在△ABC 中，∠ACB＝90，D、E 分别在 AC、AB 边上，把△ADE 沿 DE 翻折得到△FDE，点 F 恰好落在 BC 边上，若△CFD 与△BFE 都是等腰三角形， 则∠BAC 的度数为_________．

Answer 1

【答案】45°或60°

【解析】

根据题意画出图形，设∠BAC的度数为x，则∠B=90°-x，∠EFB =135°-x，∠BEF=2x-45°，

当△BFE 都是等腰三角形，分三种情况讨论，即可求解.

∵∠ACB＝90，△CFD是等腰三角形，

∴∠CDF=∠CFD=45°，

设∠BAC的度数为x，

∴∠B=90°-x，

∵△ADE 沿 DE 翻折得到△FDE，点 F 恰好落在 BC 边上，

∴∠DFE=∠BAC=x，

∴∠EFB=180°-45°-x=135°-x，

∵∠ADE=∠FDE，

∴∠ADE=（180°-45°）÷2=67.5°，

∴∠AED=180°-∠ADE-∠BAC=180°-67.5° -x=112.5°-x，

∴∠DEF=∠AED=112.5°-x，

∴∠BEF=180°-∠AED-∠DEF=180°-（112.5°-x）-（112.5°-x）=2x-45°，

∵△BFE 都是等腰三角形，分三种情况讨论：

①当FE=FB时，如图1，

则∠BEF=∠B，

∴90-x=2x-45，解得：x=45；

②当BF=BE时，

则∠EFB=∠BEF，

∴135-x=2x-45，

解得：x=60，

③当EB=EF时，如图2，

则∠B=∠EFB，

∴135-x=90-x，无解，

∴这种情况不存在.

综上所述：∠BAC 的度数为：45°或60°.

故答案是：45°或60°.

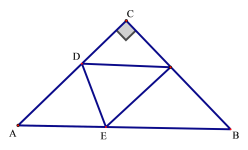
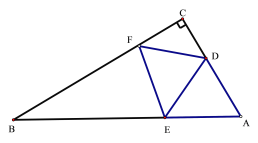
图1 图 2