题目内容

观察算式：
1+3=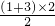数学公式，1+3+5=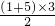数学公式，1+3+5+7=数学公式…
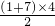按规律填空：
（1）1+3+5+7+9+…+99=______．
（2）1+3+5+7+9+…+（2n-1）=______．

解：（1）1+3+5+7+9+…+99==2500；

（2）1+3+5+7+9+…+（2n-1）==n2．
故答案为；．
分析：观察所给的算式都是计算从1开始的连续奇数的和，它们的和为把首尾两个奇数相加乘以奇数的个数除以2，利用此规律分别进行计算即可．
点评：本题考查了规律型：数字的变化类：通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．
练习册系列答案
相关题目
观察算式：
1
1×2
=1-
1
2
，
1
2×3
=
1
2
-
1
3
，
1
3×4
=
1
3
-
1
4
，并以此规律计算：
1
1×2
+
1
2×3
+
1
3×4
+…+
1
2007×2008
．
观察算式：
1
1×2
=1-
1
2
=
1
2

1
1×2
+
1
2×3
=1-
1
2
+
1
2
-
1
3
=
2
3

1
1×2
+
1
2×3
+
1
3×4
=1-
1
2
+
1
2
-
1
3
+
1
3
-
1
4
=
3
4

（1）按规律填空
1
1×2
+
1
2×3
+
1
3×4
+
1
4×5
+
1
5×6
=
 

1
1×2
+
1
2×3
+
1
3×4
+
1
4×5
+…+
1
99×100
=
 

（2）若n为正整数，化简：
1
n(n+1)
+
1
(n+1)(n+2)
+
1
(n+2)(n+3)
+
1
(n+3)(n+4)
+…+
1
(n+99)(n+100)
，并写出求解过程．
观察算式：
1
1×2
=1-
1
2
=
1
2
，
1
1×2
+
1
2×3
=1-
1
2
+
1
2
-
1
3
=
2
3
，
1
1×2
+
1
2×3
+
1
3×4
=1-
1
2
+
1
2
-
1
3
+
1
3
-
1
4
=
3
4
；
…
（1）按规律填空：
①
1
1×2
+
1
2×3
+
1
3×4
+
1
4×5
=
4
5
4
5
；
②
1
1×2
+
1
2×3
+
1
3×4
+
1
4×5
+…+
1
99×100
=
99
100
99
100
；
③如果n为正整数，那么
1
1×2
+
1
2×3
+
1
3×4
+
1
4×5
+…+
1
n×(n+1)
=
n
n+1
n
n+1
；
（2）计算（由此拓展写出具体过程）：
①
1
1×3
+
1
3×5
+
1
5×7
+…+
1
99×101
；
②1-
1
2
-
1
6
-
1
12
-…-
1
9900
．
观察算式：
1
1×2
=1-
1
2
=
1
2

1
1×2
+
1
2×3
=1-
1
2
+
1
2
-
1
3
=
2
3

1
1×2
+
1
2×3
+
1
3×4
=1-
1
2
+
1
2
-
1
3
+
1
3
-
1
4
=
3
4

按规律填空 
1
1×2
+
1
2×3
+
1
3×4
+
1
4×5
=
4
5
4
5

1
1×2
+
1
2×3
+
1
3×4
+
1
4×5
+
1
5×6
=
5
6
5
6

1
1×2
+
1
2×3
+
1
3×4
+
1
4×5
+…+
1
99×100
=
99
100
99
100

若n为正整数，试求：
1
n(n+1)
+
1
(n+1)(n+2)
+
1
(n+2)(n+3)
+
1
(n+3)(n+4)
+…+
1
(n+99)(n+100)
的值，并写出求值过程．
观察算式：
1
1×2
=1-
1
2
=
1
2
，
1
1×2
+
1
2×3
=1-
1
2
+
1
2
-
1
3
=
2
3

1
1×2
+
1
2×3
+
1
3×4
=1-
1
2
+
1
2
-
1
3
+
1
3
-
1
4
=
3
4

按规律填空
1
1×2
+
1
2×3
+
1
3×4
+
1
4×5
=
4
5
4
5
；
1
1×2
+
1
2×3
+
1
3×4
+
1
4×5
+…+
1
99×100
=
99
100
99
100
；
如果n为正整数，那么
1
1×2
+
1
2×3
+
1
3×4
+
1
4×5
+…+
1
n(n+1)
=
n
n+1
n
n+1
．
由此拓展写出具体过程，
1
1×3
+
1
3×5
+
1
5×7
+…+
1
99×101
═

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网