题目内容
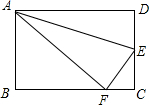如图，将长方形ABCD沿AE折叠，使点D落在BC边上的点F，若∠DAE=15°，则∠BAF=
- A.15°
- B.30°
- C.45°
- D.60°
D
分析：根据翻折的性质可得∠EAF=∠DAE，再根据长方形的每一个角都是直角列式进行计算即可得解．
解答：∵△AEF是△ADE沿AE折叠得到，∠DAE=15°，
∴∠EAF=∠DAE=15°，
在长方形ABCD中，∠BAF=90°-∠EAF-∠DAE=90°-15°-15°=60°．
故选D．
点评：本题考查了角的计算，翻折变换的性质，是基础题，掌握翻折前后的两个角相等是解题的关键．
分析：根据翻折的性质可得∠EAF=∠DAE，再根据长方形的每一个角都是直角列式进行计算即可得解．
解答：∵△AEF是△ADE沿AE折叠得到，∠DAE=15°，
∴∠EAF=∠DAE=15°，
在长方形ABCD中，∠BAF=90°-∠EAF-∠DAE=90°-15°-15°=60°．
故选D．
点评：本题考查了角的计算，翻折变换的性质，是基础题，掌握翻折前后的两个角相等是解题的关键．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
相关题目
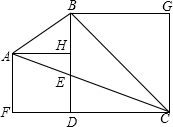如图，将面积为a2的小正方形和面积为b2的大长方形放在一起（a＞0，b＞0），求三角形ABC的面积．
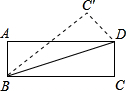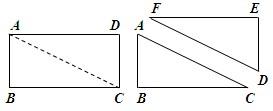
如图，将长方形ABCD沿对角线BD折叠，使点C恰好落在如图C′的位置，若∠DBC=15°，则∠ABC′=（ ）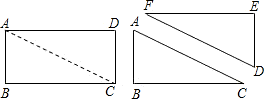
如图，将长方形ABCD沿对角线AC剪开，得到两个三角形为△ABC和△DEF．若将△DEF经过不同的变换，使得△ABC和△DEF有一条边重合，这样得到的不同的三角形有
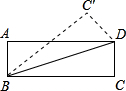如图，将长方形ABCD沿对角线BD折叠，使点C恰好落在如图C′的位置，若∠DBC=15°，则∠ABC′=