题目内容
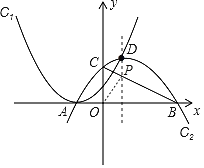
【题目】如图,抛物线C1:y=(x+![]() )2,平移抛物线y=﹣x2,使其顶点D在抛物线C1位于y轴右侧的图象上,得到抛物线C2,抛物线C2交x轴于A、B两点(点A在点B的左侧),交y轴于点C,设点D的横坐标为a.
)2,平移抛物线y=﹣x2,使其顶点D在抛物线C1位于y轴右侧的图象上,得到抛物线C2,抛物线C2交x轴于A、B两点(点A在点B的左侧),交y轴于点C,设点D的横坐标为a.

(1)当OC=2时,求抛物线C2的解析式;
(2)在抛物线的C2的对称轴上是否存在一点P,使得AP+CP的长最短?若存在,求出点P的坐标(用含a的代数式表示);若不存在,请说明理由;
(3)在(2)的条件下,连接OP,若OP⊥BC,求此时a的值.
【答案】(1)y=﹣x2+![]() x+2;(2)存在,点P(a,
x+2;(2)存在,点P(a,![]() a+
a+![]() );(3)a=
);(3)a=![]() .
.
【解析】
(1)抛D在抛物线C1位于y轴右侧的图象上,则点D[a,(a![]() )2],则抛物线C2的表达式为:y=﹣(x﹣a)2+(a
)2],则抛物线C2的表达式为:y=﹣(x﹣a)2+(a![]() )2=﹣x2+2ax+(a
)2=﹣x2+2ax+(a![]() ),即可求解;
),即可求解;
(2)点B是点A关于对称轴的对称点,则BC交函数对称轴于点P,点P为所求点,即可求解;
(3)OP⊥BC,直线BC的表达式为:y![]() x+(a
x+(a![]() ),则直线OP的表达式中的k值为2,即可求解.
),则直线OP的表达式中的k值为2,即可求解.
(1)抛D在抛物线C1位于y轴右侧的图象上,则点D[a,(a![]() )2],则抛物线C2的表达式为:y=﹣(x﹣a)2+(a
)2],则抛物线C2的表达式为:y=﹣(x﹣a)2+(a![]() )2=﹣x2+2ax+(a
)2=﹣x2+2ax+(a![]() ),OC=2=a
),OC=2=a![]() ,解得:a
,解得:a![]() ,故抛物线的表达式为:y=﹣x2
,故抛物线的表达式为:y=﹣x2![]() x+2;
x+2;
(2)点B是点A关于对称轴的对称点,则BC交函数对称轴于点P,点P为所求点.
点A(![]() ,0),则点B(2a
,0),则点B(2a![]() ,0),点C(0,a
,0),点C(0,a![]() ),将点B、C的坐标代入一次函数表达式并解得:直线BC的表达式为:y
),将点B、C的坐标代入一次函数表达式并解得:直线BC的表达式为:y![]() x+(a
x+(a![]() ),当x=a时,y
),当x=a时,y![]() a
a![]() ,故点P(a,
,故点P(a,![]() a
a![]() );
);
(3)OP⊥BC,直线BC的表达式为:y![]() x+(a
x+(a![]() ),则直线OP的表达式中的k值为2,即:
),则直线OP的表达式中的k值为2,即: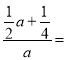 2,解得:a
2,解得:a![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目