题目内容
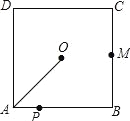
【题目】如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A﹣B﹣M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是( ).
A.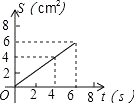 B.
B.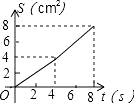
C.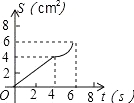 D.
D.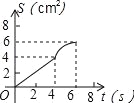
【答案】A.
【解析】
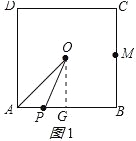
试题分析:分两种情况:①当0≤t<4时,作OG⊥AB于G,如图1所示,由正方形的性质得出∠B=90°,AD=AB=BC=4cm,AG=BG=OG=![]() AB=2cm,由三角形的面积得出S=
AB=2cm,由三角形的面积得出S=![]() APOG=t(
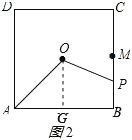
APOG=t(![]() );②当t≥4时,作OG⊥AB于G,如图2所示,S=△OAG的面积+梯形OGBP的面积=
);②当t≥4时,作OG⊥AB于G,如图2所示,S=△OAG的面积+梯形OGBP的面积=![]() ×2×2+
×2×2+![]() (2+t﹣4)×2=t(
(2+t﹣4)×2=t(![]() );综上所述:面积S(
);综上所述:面积S(![]() )与时间t(s)的关系的图象是过原点的线段.
)与时间t(s)的关系的图象是过原点的线段.
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目