题目内容
【题目】平面直角坐标系xOy中,点P的坐标为(m+1,m﹣1).
(1)试判断点P是否在一次函数y=x﹣2的图象上,并说明理由;
(2)如图,一次函数y=﹣ ![]() x+3的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围.
x+3的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围.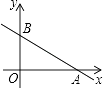
【答案】
(1)解:∵当x=m+1时,y=m+1﹣2=m﹣1,
∴点P(m+1,m﹣1)在函数y=x﹣2图象上.
(2)解:∵函数y=﹣ ![]() x+3,
x+3,
∴A(6,0),B(0,3),
∵点P在△AOB的内部,
∴0<m+1<6,0<m﹣1<3,m﹣1<﹣ ![]() (m+1)+3
(m+1)+3
∴1<m< ![]() .
.
【解析】(1)把P坐标代入y=x-2解析式即可;(2)由点P在△AOB的内部可构建不等式0<m+1<6,0<m﹣1<3,m﹣1<![]() (m+1)+3,求其交集.
(m+1)+3,求其交集.
【考点精析】根据题目的已知条件,利用一次函数的图象和性质的相关知识可以得到问题的答案,需要掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,其中的20m3仍按2元/m3计算,超过部分按2.6元/m3计算.设某户家庭月用水量xm3.
月份 | 4月 | 5月 | 6月 |
用水量 | 15 | 17 | 21 |
(1)用含x的式子表示:
当0≤x≤20时,水费为 元;
当x>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(x>6且x<14,单位:km):
第一次 | 第二次 | 第三次 | 第四次 |
x |
| x﹣5 | 2(6﹣x) |
(1)写出这辆出租车每次行驶的方向;
(2)求经过连续4次行驶后,这辆出租车所在的位置(结果可用x表示);
(3)这辆出租车一共行驶了多少路程(结果用x表示)?