题目内容
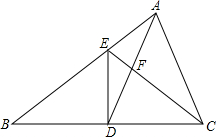 在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.
在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.(1)求证:△ABC∽△FCD;
(2)若DE=3,BC=8,求△FCD的面积.
考点:相似三角形的判定与性质
专题:
分析:(1)由DE⊥BC,D是BC的中点,根据线段垂直平分线的性质,可得BE=CE,又由AD=AC,易得∠B=∠DCF,∠FDC=∠ACB,即可证得△ABC∽△FCD;
(2)首先过A作AG⊥CD,垂足为G,易得△BDE∽△BGA,可求得AG的长,继而求得△ABC的面积,然后由相似三角形面积比等于相似比的平方,求得△FCD的面积.
(2)首先过A作AG⊥CD,垂足为G,易得△BDE∽△BGA,可求得AG的长,继而求得△ABC的面积,然后由相似三角形面积比等于相似比的平方,求得△FCD的面积.
解答: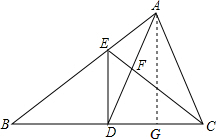 (1)证明:∵D是BC的中点,DE⊥BC,
(1)证明:∵D是BC的中点,DE⊥BC,
∴BE=CE,
∴∠B=∠DCF,
∵AD=AC,
∴∠FDC=∠ACB,
∴△ABC∽△FCD;
(2)解:过A作AG⊥CD,垂足为G.
∵AD=AC,
∴DG=CG,
∴BD:BG=2:3,
∵ED⊥BC,
∴ED∥AG,
∴△BDE∽△BGA,
∴ED:AG=BD:BG=2:3,
∵DE=3,
∴AG=
,
∵△ABC∽△FCD,BC=2CD,
∴
=(
)2=
.
∵S△ABC=
×BC×AG=
×8×
=18,
∴S△FCD=
S△ABC=
.
 (1)证明:∵D是BC的中点,DE⊥BC,
(1)证明:∵D是BC的中点,DE⊥BC,∴BE=CE,
∴∠B=∠DCF,
∵AD=AC,
∴∠FDC=∠ACB,
∴△ABC∽△FCD;
(2)解:过A作AG⊥CD,垂足为G.
∵AD=AC,
∴DG=CG,
∴BD:BG=2:3,
∵ED⊥BC,
∴ED∥AG,
∴△BDE∽△BGA,
∴ED:AG=BD:BG=2:3,
∵DE=3,
∴AG=
| 9 |
| 2 |
∵△ABC∽△FCD,BC=2CD,
∴
| S△FCD |
| S△ABC |
| CD |
| BC |
| 1 |
| 4 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∴S△FCD=
| 1 |
| 4 |
| 9 |
| 2 |
点评:此题考查了相似三角形的判定与性质以及等腰三角形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
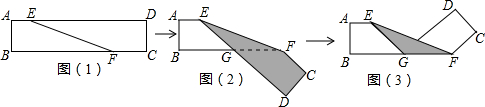
如图(1)是长方形纸带,∠DEF=α,将纸带沿EF折叠成图(2),再沿BF折叠成图(3),则图(3)中的∠CFE的度数是( )

| A、2α |
| B、90°+2α |
| C、180°-2α |
| D、180°-3α |
在平面直角坐标系xOy中,点P(2,1)关于y轴对称的点的坐标是( )
| A、(-2,1) |
| B、(2,1) |
| C、(-2,-1) |
| D、(2,-1) |
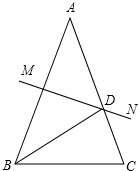 如图,在△ABC中,∠ABC=∠C,线段AB的垂直平分线MN交AC于点D.
如图,在△ABC中,∠ABC=∠C,线段AB的垂直平分线MN交AC于点D.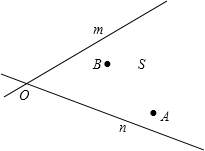 如图,电信部门要在公路m,n之间的S区域修建一座电视信号发射塔P.按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路m,n的距离也必须相等.发射塔P建在什么位置?在图中用尺规作图的方法作出它的位置并标出(不写作法但保留作图痕迹).
如图,电信部门要在公路m,n之间的S区域修建一座电视信号发射塔P.按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路m,n的距离也必须相等.发射塔P建在什么位置?在图中用尺规作图的方法作出它的位置并标出(不写作法但保留作图痕迹).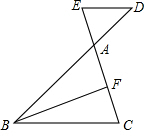 如图,点D、E分别在△ABC的边BA、CA的延长线上,且DE∥BC,
如图,点D、E分别在△ABC的边BA、CA的延长线上,且DE∥BC,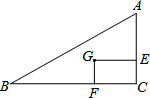 如图,点G是Rt△ABC的重心,过点G作矩形GECF,当GF:GE=1:2时,则∠B的正切值为
如图,点G是Rt△ABC的重心,过点G作矩形GECF,当GF:GE=1:2时,则∠B的正切值为