题目内容
如图,在直角坐标系中,O是坐标原点,点A的坐标是(1,| 3 |
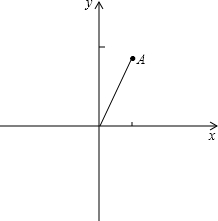 点O逆时针旋转120°,可得线段OB.
点O逆时针旋转120°,可得线段OB.(1)求点B的坐标;
(2)某二次函数的图象经过A、O、B三点,求该函数的解析式;
(3)在第(2)小题所求函数图象的对称轴上,是否存在点P,使△OAP的周长最小,若存在,求点P的坐标;若不存在,请说明理由.
分析:(1)根据点A的坐标易知∠AOx=60°,若将OA逆时针旋转120°,点A的对应点B则正好落在x轴负半轴上,易求得OA的长,即可得到OB的长,从而求出点B的坐标.
(2)已知了函数图象上三点的坐标,可利用待定系数法求得该抛物线的解析式.
(3)在△OAP中,OA的长是定值,若三角形的周长最小,那么AP+OP的值最小;由于O、B关于抛物线的对称轴对称,若连接AB,那么直线AB与抛物线对称轴的交点即为所求的点P,易求得直线AB的解析式,联立抛物线对称轴,即可求得点P的坐标.
(2)已知了函数图象上三点的坐标,可利用待定系数法求得该抛物线的解析式.
(3)在△OAP中,OA的长是定值,若三角形的周长最小,那么AP+OP的值最小;由于O、B关于抛物线的对称轴对称,若连接AB,那么直线AB与抛物线对称轴的交点即为所求的点P,易求得直线AB的解析式,联立抛物线对称轴,即可求得点P的坐标.
解答:解:(1)作AC⊥x轴于C,
∵点A(1,
),即OC=1,AC=
,
∴∠AOC=60°,OA=2;(1分)
∴点B(-2,0).(2分)
(2)∵抛物线经过点O(0,0),
∴可设所求解析式为y=ax2+bx.
把点A、B的坐标代入上式,得:
,(3分)
解得a=
,b=
;
∴所求解析式为y=
x2+
x.(4分)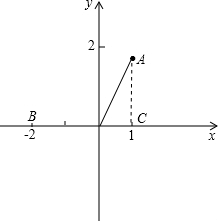
(3)存在,
∵点O和B关于抛物线y=
x2+
x的对称轴直线x=-1对称,
∴直线AB与直线x=-1的交点即为所求点P;(5分)
把点A(1,
)、B(-2,0)分别代入y=kx+b,
可求得直线AB的解析式为:y=
x+
,(6分)
令x=-1,得y=
;
∴点P(-1,
).(7分)
∵点A(1,
| 3 |
| 3 |
∴∠AOC=60°,OA=2;(1分)
∴点B(-2,0).(2分)
(2)∵抛物线经过点O(0,0),
∴可设所求解析式为y=ax2+bx.
把点A、B的坐标代入上式,得:
|
解得a=
| ||
| 3 |
2
| ||
| 3 |
∴所求解析式为y=
| ||
| 3 |
2
| ||
| 3 |

(3)存在,
∵点O和B关于抛物线y=
| ||
| 3 |
2
| ||
| 3 |
∴直线AB与直线x=-1的交点即为所求点P;(5分)
把点A(1,
| 3 |
可求得直线AB的解析式为:y=
| ||
| 3 |
2
| ||
| 3 |
令x=-1,得y=
| ||
| 3 |
∴点P(-1,
| ||
| 3 |
点评:此题主要考查了图形的旋转变化、直角三角形的性质、二次函数解析式的确定、平面展开-最短路径等知识,属于基础题,难度适中.

练习册系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: