题目内容
正四边形内切圆与外接圆的面积比为______．
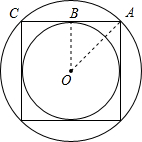
如图：连接OA，OB，
根据题意得：OB⊥AC，∠OAB=45°，
∴OB=AB，
∴OA=
=
OB，
∴OB：OA=1：
，
∴正四边形内切圆与外接圆的面积比为：π（OB）2：π（OA）2=1：2．
故答案为：1：2．
根据题意得：OB⊥AC，∠OAB=45°，
∴OB=AB，
∴OA=
| OB2+AB2 |
| 2 |
∴OB：OA=1：
| 2 |
∴正四边形内切圆与外接圆的面积比为：π（OB）2：π（OA）2=1：2．
故答案为：1：2．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
