题目内容

已知D、E分别是△ABC的AB、AC中点，则S_△ADE：S_{四边形DBCE}=________．

$\text{[math]}$
分析：根据D、E分别是△ABC的AB、AC中点，利用三角形中位线定理求证△ADE∽△ABC，然后利用相似三角形面积比等于相似比的平方即可解题．
解答：

解：∵D、E分别是△ABC的AB、AC中点，
∴△ADE∽△ABC，
∴ $\text{[math]}$ = $\text{[math]}$ ，
∴ $\text{[math]}$ = $\text{[math]}$ ，
∴ $\text{[math]}$ = $\text{[math]}$ ．
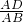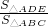故填： $\text{[math]}$ ．
点评：此题考查学生对相似三角形的判定与性质和三角形中位线定理的理解和掌握，解答此题的关键是利用相似三角形面积比等于相似比的平方．

练习册系列答案

浙江新课程三维目标测评课时特训系列答案

蓉城学堂课课练系列答案

先锋课堂导学案系列答案

名牌小学课时作业系列答案

励耘书业浙江期末系列答案

周周清检测系列答案

智慧课堂好学案系列答案

轻巧夺冠周测月考直通高考系列答案

易百分初中同步训练方案系列答案

百分导学系列答案

相关题目

已知D、E分别是△ABC的边AB、AC的中点，DE=2，那么BC的长是（　　）

作图题
（1）如图1，已知?ABCD两边长分别是1和2，一个内角为60°，将?ABCD剪一刀成两部分，并拼成一个等腰三角形．要求在原图上画出剪切线和组成的等腰三角形，并填写等腰三角形的周长（本题不限作图工具）

（2）如图2，已知正方形ABCD边长为2，将正方形剪两刀成三部分，并拼成一个等腰非直角三角形，要求在原图上画出剪切线和拼成的三角形，并填出等腰三角形的周长．

邻边不相等的矩形纸片，剪去一个正方形，余下一个四边形，称为第一次操作；在余下的四边形中减去一个正方形，又余下一个四边形，称为第二次操作；…，以此类推，若第n次操作后余下的四边形是正方形，则称原矩形是n阶矩形．如图1，矩形ABCD中，若AB=1，AD=2，则矩形ABCD是1阶矩形．

探究：（1）两边分别是2和3的矩形是

阶矩形；
（2）小聪为了剪去一个正方形，进行如下的操作：如图2，把矩形ABCD沿着BE折叠（点E在AD上），使点A落在BC的点F处，得到四边形ABFE．请证明四边形ABFE是正方形．
（3）操作、计算：
①已知矩形的两边分别是2，a（a＞2），而且它是3阶矩形，请画出此矩形及裁剪线的示意图，并在示意图下方直接写出a的值；
②已知矩形的两邻边长为a，b，（a＞b），且满足a=5b+m，b=4m．请直接写出矩形是几阶矩形．

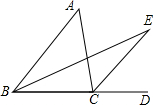如图，已知BE、CE分别是△ABC的内角、外角的平分线，∠A=40°，求∠E的度数．

已知三角形的两边分别是3和4，第三边长是方程x²-6x+5=0的根，试判断这个三角形的形状．