��Ŀ����
����Ŀ���ۺ���̽��
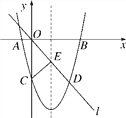
��ͼ����ƽ��ֱ������ϵ�У���֪������y��ax2��bx��8��x�ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��l��������ԭ��O���������ߵ�һ������ΪD���������ߵĶԳ��ύ�ڵ�E������CE����֪��A��D������ֱ�Ϊ(��2��0)��(6����8)��
(1)�������ߵĽ���ʽ�����ֱ������B�͵�E�����ꣻ
(2)��̽�����������Ƿ���ڵ�F��ʹ��FOE�ա�FCE.�����ڣ���ֱ��д����F�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1) y��![]() x2��3x��8����2����F������Ϊ(3��
x2��3x��8����2����F������Ϊ(3��![]() ����4)��(3��
����4)��(3��![]() ����4)��
����4)��
�������������������1����A��D������������߿���������ߵĺ�������ʽ���������ߵĶԳ��Կ����B�����꣬��D����������ֱ��OD�Ľ���ʽ��������E�����ꣻ
��2����ϣ�1����֪OE=CE����ȫ�������ε����ʿ�֪OF=CF����֪��F���߶�OC�Ĵ�ֱƽ�����ϣ�������F��������꣬���������߽���ʽ�����F������꣮
���������
��1����������y=ax2+bx-8������A��-2��0����D��6��-8����
��![]()
���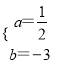
�������ߵĺ�������ʽΪy��![]() x23x8��
x23x8��
��y��![]() x23x8��
x23x8��![]() (x3)2
(x3)2![]() ��
��
�������ߵĶԳ���Ϊֱ��x=3��
����������x�ύ��A��B���㣬��A������Ϊ��-2��0����
���B��������8��0����
��ֱ��L�ĺ�������ʽΪy=kx��
�ߵ�D��6��-8����ֱ��L�ϣ�
��6k=-8�����k=-![]() ��
��
��ֱ��L�ĺ�������ʽΪy=-![]() x��
x��
�ߵ�EΪֱ��L�������߶Գ���Ľ��㣬
���E�ĺ�����Ϊ3��������Ϊ-![]() ��3=-4��
��3=-4��
���E��������3��-4����
��2���������ϴ��ڵ�F��ʹ��FOE�ա�FCE��
��OE=CE=5��
��FO=FC��
���F��OC�Ĵ�ֱƽ�����ϣ���ʱ��F��������Ϊ-4��
��![]() x2-3x-8=-4�����x=3��
x2-3x-8=-4�����x=3��![]() ��
��
���F��������3-![]() ��-4����3+
��-4����3+![]() ��-4����
��-4����

 ��У����ϵ�д�
��У����ϵ�д�